The MCMC Diagnostics add-in calculates convergence diagnostics as well as equal-tailed and HPD credible intervals for a data set containing posterior samples from one or more parallel Markov chains. Included are two posterior probability calculators. This add-in does not perform MCMC but allows for straightforward analysis and review of posterior samples.
The dialog below displays an example for 60,000 MCMC samples for 3 independently run Markov chains from a Bayesian hierarchical model of 40 adverse events from Mehrotra & Heyse (2004). The independent Markov chains are provided so that Gelman-Rubin diagnostics are computed.
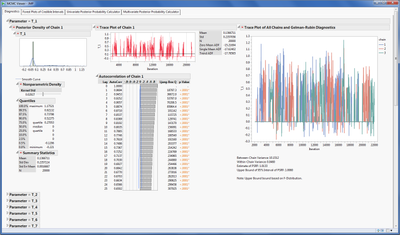
The figure below shows the Diagnostics panel where each parameter is summarized using several graphs and analyses. These analyses include
- Histogram with non-parametric density curve and summary statistics for chain 1
- Trace plot of MCMC samples for chain 1
- Plots and tests to assess autocorrelation of samples across time for chain 1
- If multiple chains are provided, a trace plot of all chains to assess convergence is provided along with Gelman-Rubin diagnostics
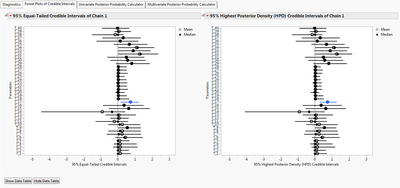
Forest plots containing equal-tailed and highest posterior density (HPD) credible intervals are provided for chain 1.
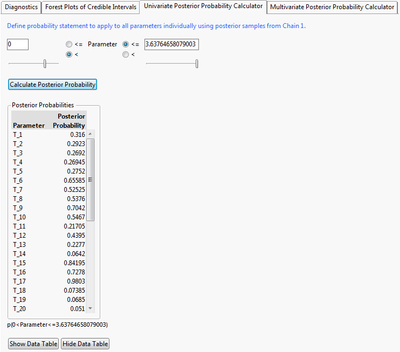
A univariate probability calculator is provided to calculate the probability that each parameter is within the supplied range. Here, I calculate the probability that the parameter is positive, which would indicate that there is excess risk on the novel treatment.
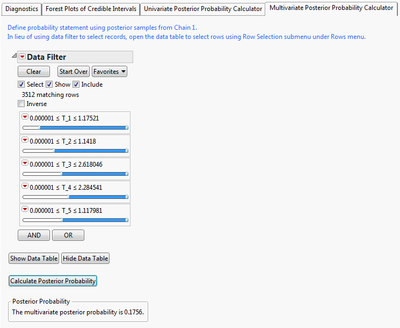
The multivariate probability calculator lets you calculate when sets of parameters meet criteria jointly. Here, I calculate the probability that the first five parameters are simultaneously positive. This can be interpreted as the probability that the first five adverse events show excess risk simultaneously.
Go to support.sas.com/resources/papers/proceedings13/179-2013.pdf for more detail.
Mehrotra DV & Heyse JF. (2004). Use of the False Discovery Rate for Evaluating Clinical Safety Data. Statistical Methods in Medical Research 13: 227-238.