probit analysis - fit testing (regression) and replicates

[#1]

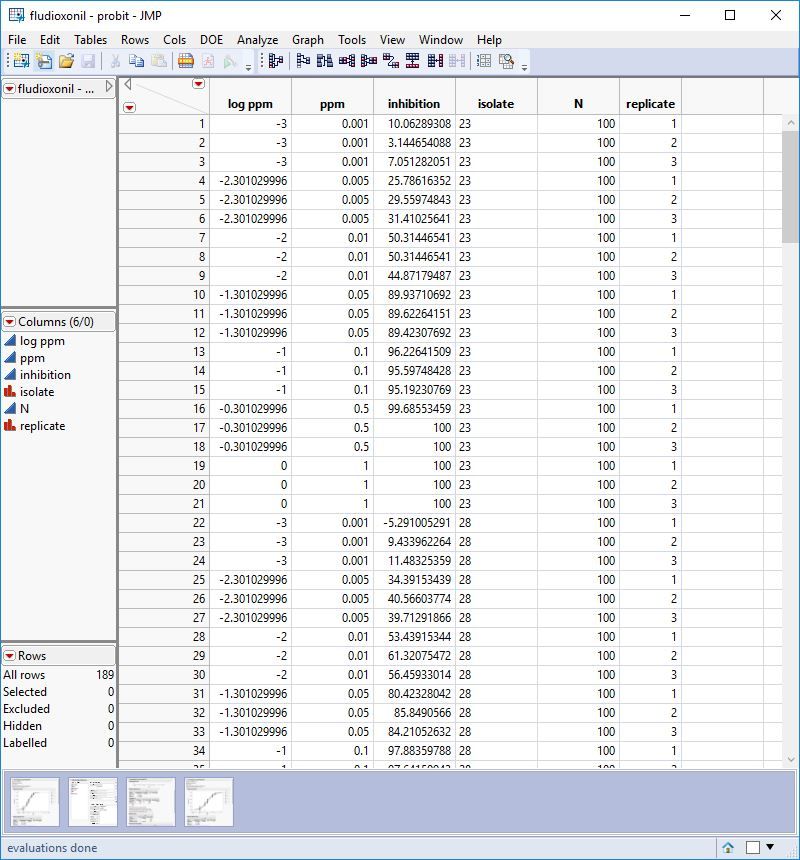
I'm trying to determine the ec50 (concentration at which there is 50% radial fungal growth compared to the control) of certain fungicides I've tried in vitro (in petri dishes) vs different isolates. I have tested the same 9 different isolates with different fungicides as radial mycelium growth. For every fungicide there are 5, 6 or 7 (depending on the fungicide) concentrations tested and 3 replicates for each concentration. For each fungicide all petri dishes were measured the same day.

The probit - binomial distribution seems to fit the data well, at least in most cases.

My issues are how to include replicates in the analysis and how determine the standard error.

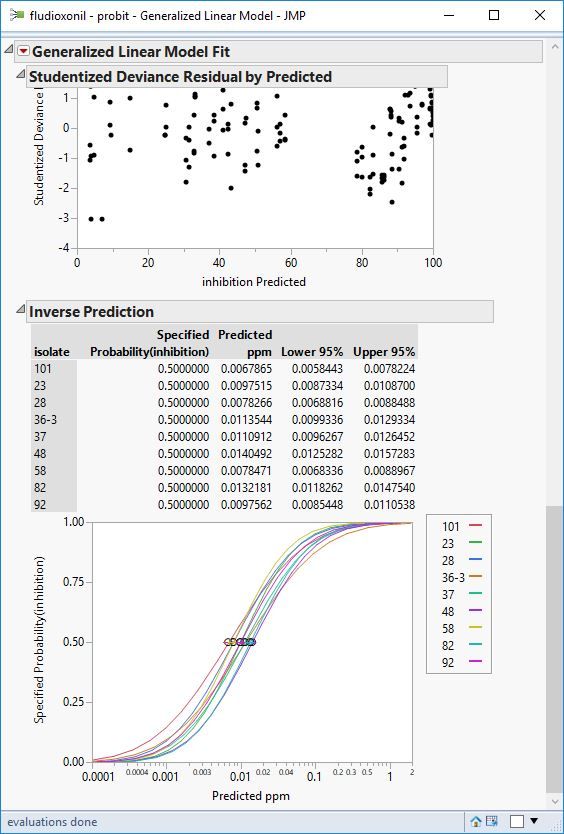
Attached are screenshots of the data.

datafit modelregression plotec 50

[#2]

In this case the group of replicates are it together. Its isn't a bad way to go, because its essentially fitting the mean replicates which results in a better fit to the response pattern. Keep in mind the replicates aren't independent observations (dependent on the experimental unit), and JMP assumes that each row is an independent observation.  If the data were stacked (one column for each replicate and one row for each isolate) 

You might also want to try to fit each replicate separately for each isolate. like this:

Just note that you have to manually add each inverse prediction for each isolate. (note: super tedious, so send a feature suggestion to support at jmp dot com) Hold down CTRL when you choose the Inverse prediction option then the dialog for calculating the 0.5 probability will come up for each isolate.

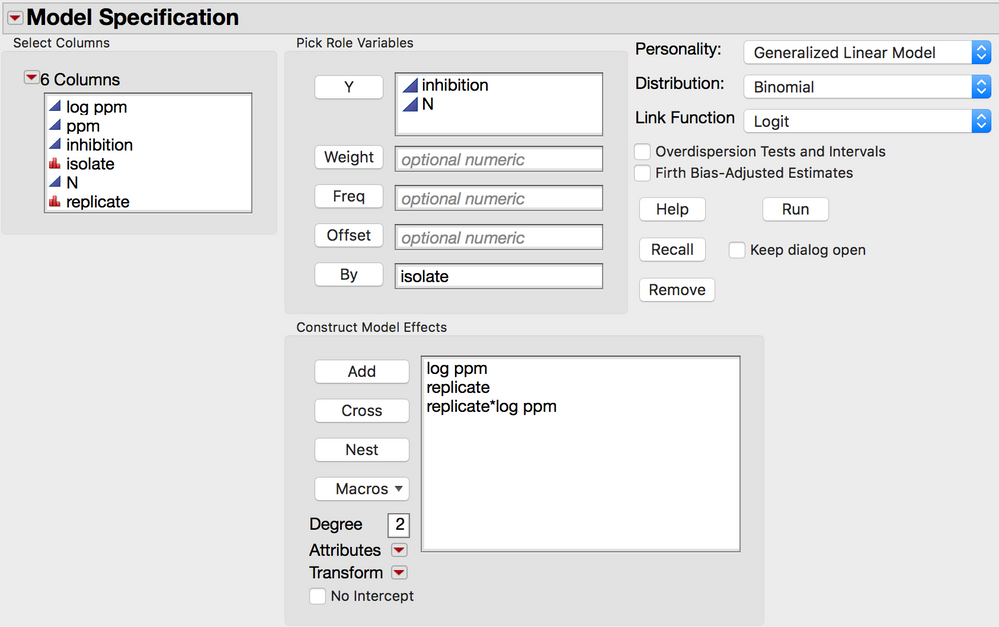
In this case the fit for each replicate by isolate will be calculated. The error is not pooled for the replcates. This is like doing a mixed model with independent estimates of sigma. 

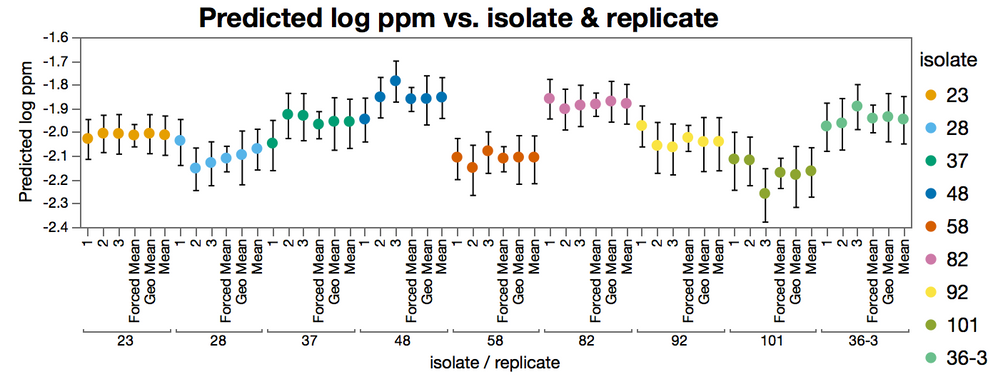
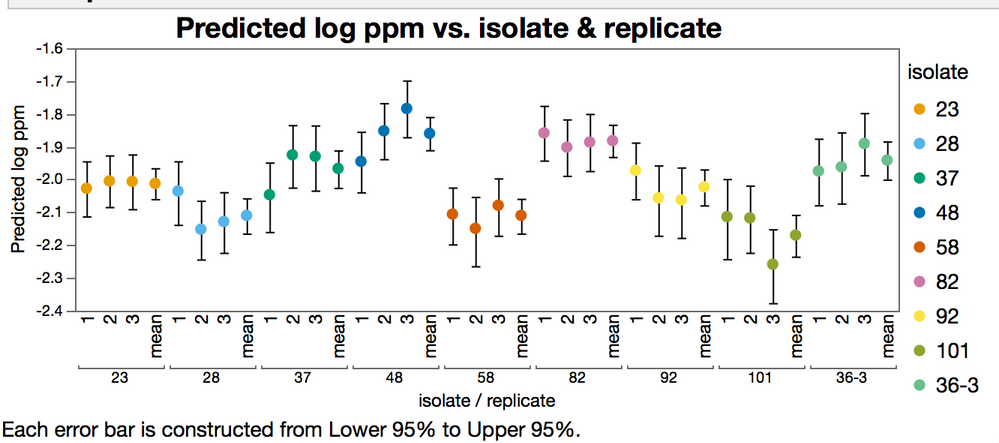
In the figure below, the "mean" level is the fit like you did in your post, with all the replicates together. Note the difference in the confidence intervals. 

note: JMP 14 has the interval role, so this easy to make.

So the issue to deal with is that if the table is in the tall format like the file that was posted, the replicates in the rows get treated like they are independent observations. I'm going to make a safe assumption that they are not independent. The replicates are dependent on the experimental unit.  So here's how to work with that.  and are An alternative approach is to split the table like this:

current Datatable() << Split(
Split By( :Replicate ),
Split( :inhibition ),
Group( :isolate, :ppm ),
Sort by Column Property
);

Not sure which is the best was to treat the replicates, either Average or Geometric Mean?

But either way, it is easy to see that the confidence intervals for the forced mean (table in the tall format with independent replicates.)  are a lot narrower than the interval of the means from the split table. This is because the degrees of freedom are inflated by treating the replicates as being indepentdent. 

The data for this graph is from the EC50s of the data fit in different ways, its not a default report graph.

[#3]

Thank you. Could you please tell me how you calculated the averages? Did you export them to a table and from there prepare the graph? I can't seem to figure it out. Thank you in advance.

[#4]

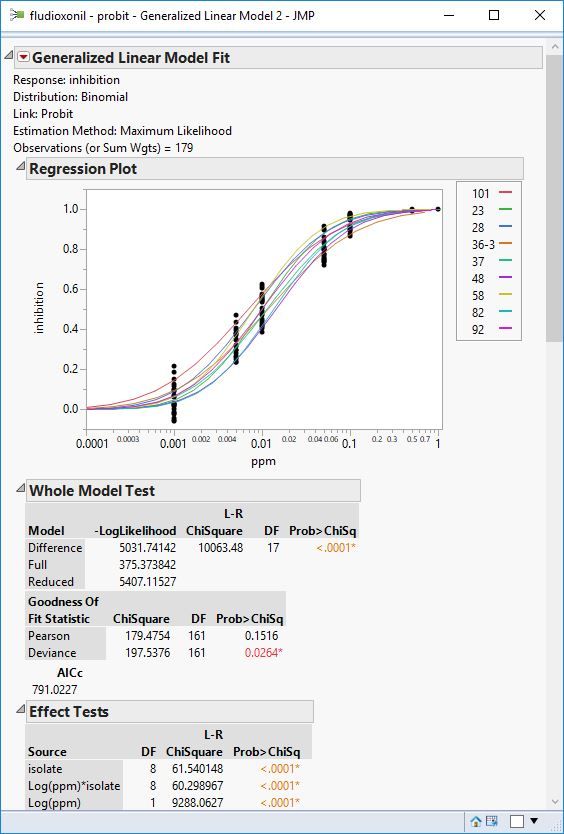
I used the inverse prediction interval option under the red triangle after I fit the model, to get the inflection points/ec50s

[#5]

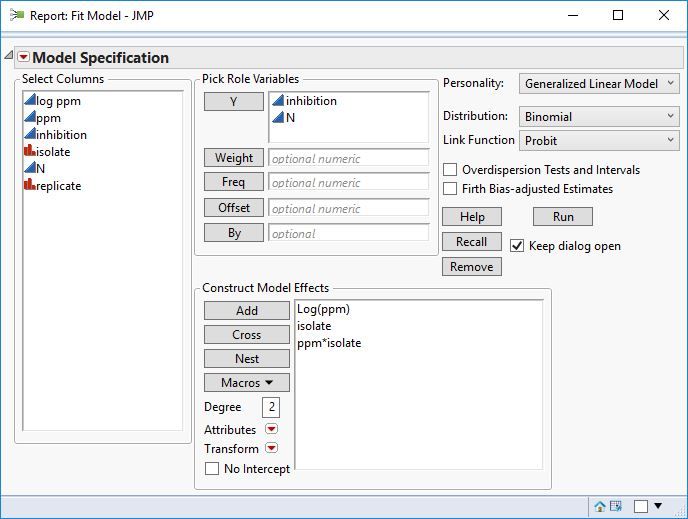
So I set up the analysis like in the figure above  (quick script below to set it up)

Fit Model(
	Y( :inhibition, :N ),
	By( :isolate ),
	Effects( :log ppm, :Replicate, :Replicate * :log ppm ),
	Personality( "Generalized Linear Model" ),
	GLM Distribution( "Binomial" ),
	Link Function( "Logit" ),
	Overdispersion Tests and Intervals( 0 ),
	Name( "Firth Bias-Adjusted Estimates" )(0),
	Run
)

Hold down the control key (command key on OSx) and while holding click on the highest level red triangle, from the menu select Inverse prediction.  Then for each dialog that pops up, enter 0.5 for the probability to predict. This takes a while because you'll be prompted for every level of isolate.   

After thats done, right click on one of the inverse prediction tables for one of the isolates, and select Make Combined Data table.    This table is the one I did the manipulation in the example above so I could graph and analyze.