- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- pooled /unpooled t test
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
pooled /unpooled t test
Hi
What is the appropriate two sample t procedure for the summary below milking periods of cow breeds pooled/unpooled (Welch) using R?
Frisian cow Xbar=342.5 S1=10.2 n1=126
Jersey cow Xbar =348.6 S2=12.2 n2=39
Construct 95% confidence interval for µ1-µ2
Give proper interpretation of the interval
Thanks
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: pooled /unpooled t test
@Alma1 , I do not know what data you have, an example would be helpful.
In the below script (when you execute) you see a dataset and both t-test performed, giving different results.
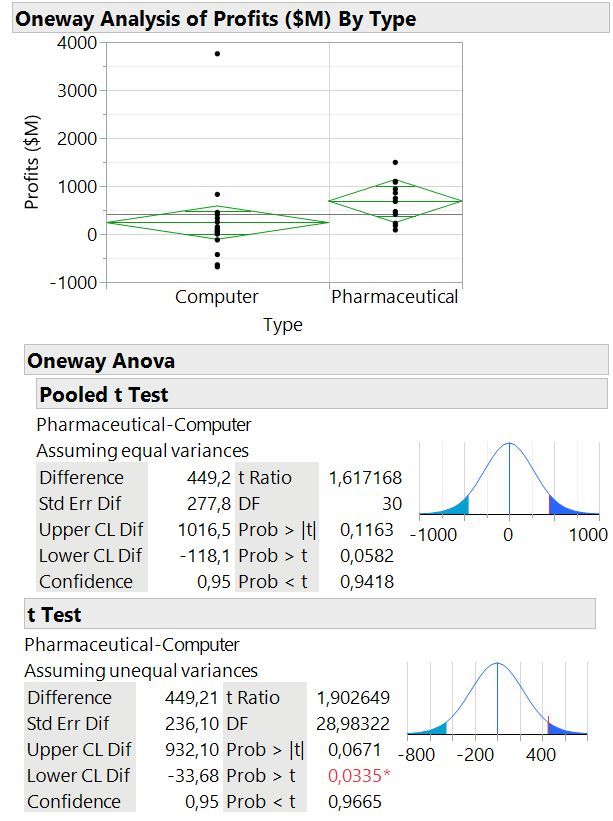
Generally, statistical Tests have preconditions, and t-test assumes normal Distribution of the dataset,
pooled t-test assumes equal variance,
t-test works also with different variance.
This is because they work with mean and variance, and if that two numbers do not represent the data correctly, the method doesn't work.
If you perform a t-test, and the assumptions are not valid, you cannot rely on the result.
In the below example you can see different results for both t-Tests, but be Aware, that normal Distribution is also not valid in this case.
You can find These results in the documentation also, and I found STIPS a quite good training to understand this stuff.
Names Default To Here( 1 );
cdt = Open( "$SAMPLE_DATA\companies.jmp" );
cdt << Oneway(
Y( :Name( "Profits ($M)" ) ),
X( :Type ),
Means( 1 ),
t Test( 1 ),
Mean Diamonds( 1 ),
SendToReport(
Dispatch( {"Oneway Anova"}, "Summary of Fit", OutlineBox, {Close( 1 )} ),
Dispatch( {"Oneway Anova"}, "Analysis of Variance", OutlineBox, {Close( 1 )} ),
Dispatch( {"Oneway Anova"}, "Means for Oneway Anova", OutlineBox, {Close( 1 )} )
)
);- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: pooled /unpooled t test
Why are you asking the JMP community to answer a question that is directed for a solution using R?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: pooled /unpooled t test
Nop! it is not a homework. we are conducting a research and I didnt know whether to use pooled /unpooled test whats wrong asking for ideas? you are free not to answer if you wish
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: pooled /unpooled t test
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: pooled /unpooled t test
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: pooled /unpooled t test
@Alma1 , I do not know what data you have, an example would be helpful.
In the below script (when you execute) you see a dataset and both t-test performed, giving different results.
Generally, statistical Tests have preconditions, and t-test assumes normal Distribution of the dataset,
pooled t-test assumes equal variance,
t-test works also with different variance.
This is because they work with mean and variance, and if that two numbers do not represent the data correctly, the method doesn't work.
If you perform a t-test, and the assumptions are not valid, you cannot rely on the result.
In the below example you can see different results for both t-Tests, but be Aware, that normal Distribution is also not valid in this case.
You can find These results in the documentation also, and I found STIPS a quite good training to understand this stuff.
Names Default To Here( 1 );
cdt = Open( "$SAMPLE_DATA\companies.jmp" );
cdt << Oneway(
Y( :Name( "Profits ($M)" ) ),
X( :Type ),
Means( 1 ),
t Test( 1 ),
Mean Diamonds( 1 ),
SendToReport(
Dispatch( {"Oneway Anova"}, "Summary of Fit", OutlineBox, {Close( 1 )} ),
Dispatch( {"Oneway Anova"}, "Analysis of Variance", OutlineBox, {Close( 1 )} ),
Dispatch( {"Oneway Anova"}, "Means for Oneway Anova", OutlineBox, {Close( 1 )} )
)
);- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: pooled /unpooled t test
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: pooled /unpooled t test
by the way jmp background is R.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: pooled /unpooled t test
@Alma1 wrote:
by the way jmp background is R.
I'm not sure exactly what you're thinking of here but JMP has no background with R.
JMP is a product from SAS and is developed solely by us.
There is integration with R through JSL, providing the ability to call R and submit R code but that's the only association between JMP and R.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: pooled /unpooled t test
I would suggest keeping up the academic value and providing help if needed instead of bothering what is asked.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us