- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Simple question: how is RMSE calculated?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Simple question: how is RMSE calculated?
Hello,
when plotting a simple regression graph I can get the R^2 and RMSE.
I would like to know how is RMSE calculated specifically in JMP.
This is because I read somewhere (Fearn 2002) that some people take the square root of the squared sum of error, devided by n while others devided by n-1.
How does JMP 13 Pro do it?
Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Simple question: how is RMSE calculated?
JMP and now JMP Pro have always computed RMSE the same way: as defined by the analysis of variance. It is the square root of the mean square error. The mean square error is the quotient of the sum of squares error divided by the degrees of freedom of the error. The degrees of freedom of the error is the degrees of freedom for the corrected total minus the degrees of freedom of the model. The degrees of freedom for the corrected total is N - 1. (The correction for the mean response costs one degree of freedom.)
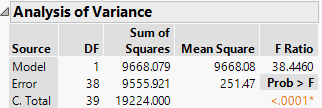
Here is a simple linear regression of weight versus height using the Big Class data table in the Sample Data folder:
The degrees of freedom for the error is DF(CT) - DF(M) = 39 - 1 = 38. A single parameter is required for height.
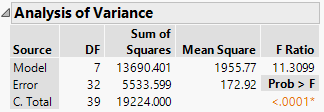
Here is a multiple regression of weight versus age, sex, and height:
The degrees of freedom for the error is DF(CT) - DF(M) = 39 - 7 = 32. Seven parameters are required for age, sex, and height.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Simple question: how is RMSE calculated?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Simple question: how is RMSE calculated?
It's actually divided by the total sample size minus the number of model terms (n - df_model). For example, if I do an ANOVA with 15 data points and 1 categorical factor with 3 levels, the model will have 1 intercept term and 2 model terms for the categorical factor (3 total). So, the RMSE will be the sqrt(SSE/(15-3)).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Simple question: how is RMSE calculated?
Root Mean Squared Error using Python sklearn Library
Mean Squared Error ( MSE ) is defined as Mean or Average of the square of the difference between actual and estimated values. This means that MSE is calculated by the square of the difference between the predicted and actual target variables, divided by the number of data points. It is always non–negative values and close to zero are better.
Root Mean Squared Error is the square root of Mean Squared Error (MSE). This is the same as Mean Squared Error (MSE) but the root of the value is considered while determining the accuracy of the model.
import numpy as np
import sklearn.metrics as metrics
actual = np.array([56,45,68,49,26,40,52,38,30,48])
predicted = np.array([58,42,65,47,29,46,50,33,31,47])
mse_sk = metrics.mean_squared_error(actual, predicted)
rmse_sk = np.sqrt(mse)
print("Root Mean Square Error :", rmse_sk)Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us