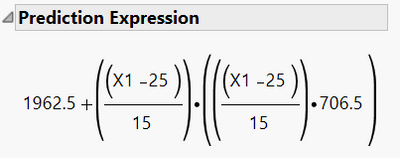- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Regression model does not provide correct quadratic equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Regression model does not provide correct quadratic equation
Hello:
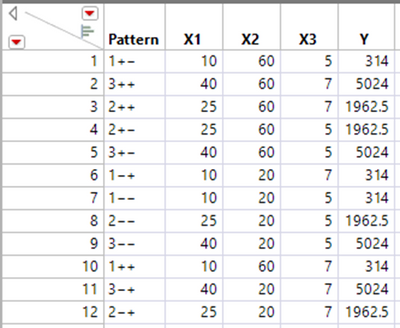
I created a 2^3 full factorial experiment with 4 center points. X1, X2 and X3 are the factors and Y is the response. X2 and X3 are just any random factor, but X1 is the radius and Y is the area. So mathematically relation is Y=3.14*X1^2
Below are the three scenarios where I computed regression equation based on just X1, both X1 and X1^2 and only X1^2.
When I only consider X1^2, it is no more significant. On further researching I came across Effect Heredity which states that we should have lower order effect included when we have higher order effect in our regression model. But than we will never be ale to find a relation that is pure quadratic as in this case.
I have also mentioned the model details that I used to analyze the data. Does different setting give me a better answer.
Please let me know if I have a serious flaw in my understanding and am doing a very basic mistake in understanding DOE.
Your help is highly appreciated.
Best Regards,
Varun Katiyar
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regression model does not provide correct quadratic equation
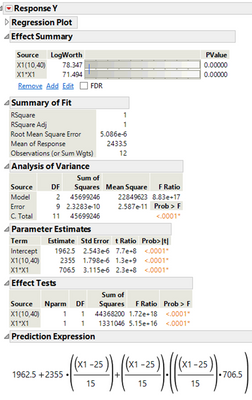
Actually, the regression coefficients are correct. You are not able to see it because of the default factor coding that JMP uses when analyzing a designed experiment.
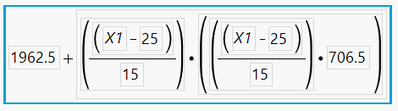
You see this prediction expression:
Notice that we should not expect the slope parameter to be 3.14 because that is not what is multiplying X^2. Instead, the 706.5 is multiplying ((x1-25)/15)*((x1-25)/15)).
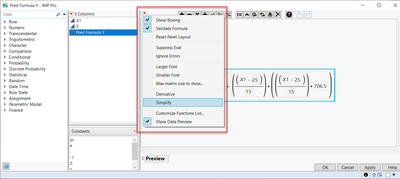
If you save that prediction formula from the red triangle and open up that formula from the data table, you will see this:
Now from the red triangle at the top (highlighted here), choose Simplify:
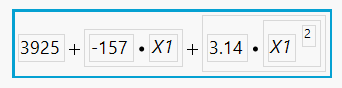
You will see the modified equation with the 3.14 that you expected.
The 3925-157*X1 appears because the model that I simplified only had the quadratic term in it. That leads to these "extra terms" that should not be part of what we know as the true model.
Now if we had fit the model following hierarchy (as recommended) and simplified this equation:
we will get exactly what you want (subject to round-off error)!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regression model does not provide correct quadratic equation
Hi @VarunK,
Learning about DoE by yourself can be very difficult, and you'll very likely encounter a lot of questions or difficulties. I would highly encourage you to learn DoE and statistics with some basic hands-on free courses :
- Design of Experiments Intro Kit
- Statistical Thinking for Industrial Problem Solving (there is a dedicated module for DoE)
- Other ressources listed in the DoE Club
Without some basic knowledge in stats and DoE, it will be very difficult to learn and understand how to use, define and apply DoE. It will also help you understand the factors coding seen in the prediction expressions.
It might also be better to practice on already defined use cases, as the one you create is not very representative on how a DoE would be used, it's more a mathematical/physical model than a research based on DoE, and may lack some attributes from DoE (effect heredity for example, no noise in the response, ...).
Or you can also practice by using the Simulate Response option in Custom design and specify a more complex model, with various degree of noise, and compare the model results with the theoritical simulated coefficients.
Also your design doesn't have "centre points" as you mention, it's only middle points for X1 (other factors X2 and X3 only have 2 levels) to estimate quadratic effects.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regression model does not provide correct quadratic equation
Hello Victor:
I already completed the Design of Experiment Kit and will try to complete the STIPS course. Having said that, I also recently completed the DOE specialization from Arizona State University through Coursera.
These all are the questions which were not directly answered and where I had some confusion on how DOE would answer them.
In the previous example that I have shared, the linear factor by itself gave me R^2 adj of 0.967, and including the quadratic term bumped it up to 1. If this relation was not know why should someone include the quadratic term?
I understand that DOE is mainly used to identify the factors and interactions that are significant and other sophisticated modeling technique might be required to gain a better relationship between the response and factor especially if quadratic effects are present.
Best Regards,
Varun Katiyar
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regression model does not provide correct quadratic equation
Actually, the regression coefficients are correct. You are not able to see it because of the default factor coding that JMP uses when analyzing a designed experiment.
You see this prediction expression:
Notice that we should not expect the slope parameter to be 3.14 because that is not what is multiplying X^2. Instead, the 706.5 is multiplying ((x1-25)/15)*((x1-25)/15)).
If you save that prediction formula from the red triangle and open up that formula from the data table, you will see this:
Now from the red triangle at the top (highlighted here), choose Simplify:
You will see the modified equation with the 3.14 that you expected.
The 3925-157*X1 appears because the model that I simplified only had the quadratic term in it. That leads to these "extra terms" that should not be part of what we know as the true model.
Now if we had fit the model following hierarchy (as recommended) and simplified this equation:
we will get exactly what you want (subject to round-off error)!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regression model does not provide correct quadratic equation
Thank you, Dan:
That was a great explanation.
Best Regards,
Varun Katiyar
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us