- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Multiplicity for Fit Model
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Multiplicity for Fit Model
How does JMP handle statistical multiplicity when running Fit Model?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiplicity for Fit Model
Multiple comparisons is a term I am familiar with, though I never do such adjustments and I'm not aware of built in capabilities for that in JMP (I certainly could be wrong about that and someone will correct me if I am). The most familiar correction is the Bonferroni correction which I'm not aware of in JMP. But it is easy enough to do by hand I think. However, I don't think it is a good idea to lower p values to account for the multiple comparisons - it does nothing to correct for dichotomous thinking that p values invite. How large is the effect size, what is the confidence interval, how many model assumptions have been made, etc. are all critical for interpreting the results of a study. When you just lower the p value, you just continue thinking that the result of a study is whether or not an effect is real, rather than the potential sizes and uncertainties about those effects.
To paraphrase Tufte's comment on pie charts (the only thing worse than one pie chart is more than one pie chart), the only thing worse than one p value is more than one p value.
Perhaps I've overstated things. But the real issue you are referring to (I believe) is subgroup analysis. Usually in RCTs, subgroup analysis is frowned upon unless it is part of the pre-registered study - in which case sampling issues have been thought of to begin with. I think a less mechanistic approach than Bonferroni is best - if you are thinking of p=.05 as denoting a strong enough effect to "matter" then if you do 20 subgroup analyses you should expect one of these to mislead you on average. In reality, you can probably expect more than one in 20 to mislead you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiplicity for Fit Model
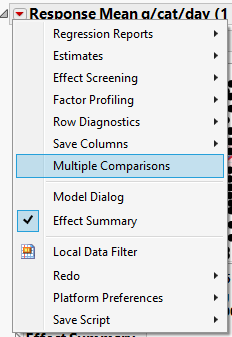
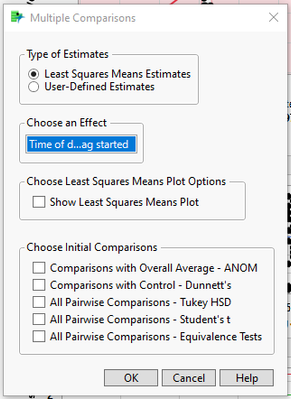
Hi @NishaKumar : OK. Yes there are several options within the Fit Model platform. Which method you choose, as you well know, depends on goals/priorities/etc. It is on the red triangle pull-down menu. See pics below.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiplicity for Fit Model
OK, I'll bite. What is "statistical multiplicity?" I've never heard the term before.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiplicity for Fit Model
Hi dlehman1:
So, statistical multiplicity is the essentially type I error or the probability of false positive. For my analysis used fit model to run odds ratios, but I need to know how it accounts for multiple comparisons/multiplicity because my dad is clinical trials and it has multiple subgroups. Below is the definition I found for multiplicity online via google:
"Multiplicity is a major consideration in the analysis of clinical trials. It occurs when multiple significance tests are carried out, increasing the family-wise error rate (FWER), the probability of a “false positive” statistically significant result or type 1 error."
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiplicity for Fit Model
*dad* I meant to write data
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiplicity for Fit Model
Hi @NishaKumar : I'm not sure what you are asking either. Do you mean multiple comparisons?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiplicity for Fit Model
Hi @MRB3855 :
Yes, it is multiple comparisons, but in clinical trials with multiple subgroups, we need to be able to account for statistical multiplicity but I am wondering if it's already accounted for with JMP's fit model? If not, how would I go about analyzing for it?
Thank you
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiplicity for Fit Model
Multiple comparisons is a term I am familiar with, though I never do such adjustments and I'm not aware of built in capabilities for that in JMP (I certainly could be wrong about that and someone will correct me if I am). The most familiar correction is the Bonferroni correction which I'm not aware of in JMP. But it is easy enough to do by hand I think. However, I don't think it is a good idea to lower p values to account for the multiple comparisons - it does nothing to correct for dichotomous thinking that p values invite. How large is the effect size, what is the confidence interval, how many model assumptions have been made, etc. are all critical for interpreting the results of a study. When you just lower the p value, you just continue thinking that the result of a study is whether or not an effect is real, rather than the potential sizes and uncertainties about those effects.
To paraphrase Tufte's comment on pie charts (the only thing worse than one pie chart is more than one pie chart), the only thing worse than one p value is more than one p value.
Perhaps I've overstated things. But the real issue you are referring to (I believe) is subgroup analysis. Usually in RCTs, subgroup analysis is frowned upon unless it is part of the pre-registered study - in which case sampling issues have been thought of to begin with. I think a less mechanistic approach than Bonferroni is best - if you are thinking of p=.05 as denoting a strong enough effect to "matter" then if you do 20 subgroup analyses you should expect one of these to mislead you on average. In reality, you can probably expect more than one in 20 to mislead you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiplicity for Fit Model
Hi @NishaKumar : OK. Yes there are several options within the Fit Model platform. Which method you choose, as you well know, depends on goals/priorities/etc. It is on the red triangle pull-down menu. See pics below.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiplicity for Fit Model
I don't think those options are available for a nominal response variable - the study being referred to results in odds ratios, so I don't think those options apply. (I might be wrong)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiplicity for Fit Model
How did you get to the response mean tab from fit model output?
What I did was go to fit model under analyze, ran it and in the output selected wald test and odds ratio. On that screen is also the FDR logsworth, but I am curious to understand how you got to the screens you provided in the screen shot please.
Thank you,
Nisha
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us