- JMP 19 is here! See the new features at jmp.com/new.
- Due to global connectivity issues impacting AWS Services, users may experience unexpected errors while attempting to authorize JMP. Please try again later or contact support@jmp.com to be notified once all issues are resolved.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Minimzation function error: "Convergence FAILURE: CANNOT DECREASE OBJECTIVE ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Minimzation function error: "Convergence FAILURE: CANNOT DECREASE OBJECTIVE FUNCTION"
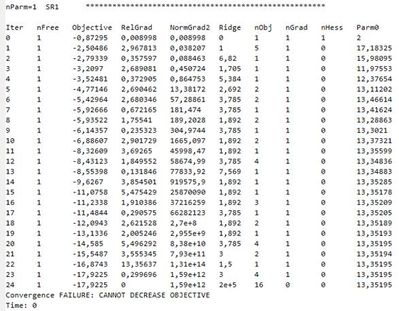
I am working on a project in JMP 16, where I use the “Minimize”-function. When running the function I often encounter the error “Convergence FAILURE: CANNOT DECREASE OBJECTIVE”. Looking at the final results of the script, they are as expected. It therefore seems that the error has little influence on the final results. However, to ensure the validity of the script, I would still like to know the reasoning behind the error. I have had difficulties finding any documentation about this specific error, and therefore hoped someone in the JMP community could help identify the cause.
Using the “<< Details( Both )” option for the minimize function, below image of the log was obtained:
Best regards,
Louis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minimzation function error: "Convergence FAILURE: CANNOT DECREASE OBJECTIVE FUNCTION"
What is the Minimize() function call that you used? What is the expression to be evaluated? What are the parameters in the expression, and how are they initialized? Is there any more information available in the JMP Log when you call this function?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minimzation function error: "Convergence FAILURE: CANNOT DECREASE OBJECTIVE FUNCTION"
Hi Mark,
Thank you for your response.
To answer your questions:
- The minimize function call is as follows:
minfun = Minimize (mfun, {df},<<UseNumericDeriv(True)); - The expression to be evaluated is as follows:
mfun = Expr( Log10( (ChiSquare Quantile( alpha, df ) / df - Vratio) ^ 2 ) ); - The parameters of the function are initilized as following:
- df: this is set to 2 before running the Minimize() function
- Both alpha and Vratio are calculated previously in the script. In the particular situation where it fails the parameters have the following values:
- alpha = 0.025
- Vratio = 0.39135
- Here it can be added, that using Vratio = 0.94917 i do not encounter the warning.
Best regards,
Louis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minimzation function error: "Convergence FAILURE: CANNOT DECREASE OBJECTIVE FUNCTION"
I used this script based on your answers.
Names Default to Here( 1 );
alpha = 0.025;
variance ratio = 0.94917 ;
df = 2;
expression = Expr( Log10( (Chi Square Quantile( alpha, df ) / df - variance ratio) ^ 2 ) );
Minimize( expression, { df( 2, 1000 ) }, << Use Numeric Deriv( "true" ) );I get the following using the two variance ratios that you gave to me:
//:*/
Names Default to Here( 1 );
alpha = 0.025;
variance ratio = 0.39135;
df = 2;
expression = Expr( Log10( (Chi Square Quantile( alpha, df ) / df - variance ratio) ^ 2 ) );
Minimize( expression, { df( 2, 1000 ) }, << Use Numeric Deriv( "true" ) );
/*:
Optimization failed: Failed: Cannot Decrease Objective Function
-19.6490758040614
//:*/
Names Default to Here( 1 );
alpha = 0.025;
variance ratio = 0.94917 ;
df = 2;
expression = Expr( Log10( (Chi Square Quantile( alpha, df ) / df - variance ratio) ^ 2 ) );
Minimize( expression, { df( 2, 1000 ) }, << Use Numeric Deriv( "true" ) );
/*:
-2.91402948948765- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minimzation function error: "Convergence FAILURE: CANNOT DECREASE OBJECTIVE FUNCTION"
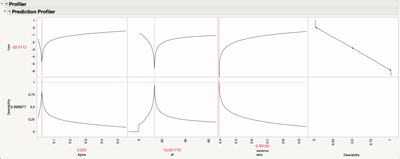
Looking at the Profiler for the function (see below, and the attached data table), it does look like Minimize() is giving a good answer.
Perhaps @chris_gotwalt1 can give an explanation of the error message you're receiving from the call to Minimize().
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minimzation function error: "Convergence FAILURE: CANNOT DECREASE OBJECTIVE FUNCTION"
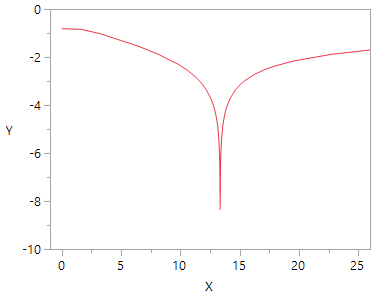
You could make a graph, like this:
expression=expr(Log10( (ChiSquare Quantile( alpha, df ) / df - Vratio) ^ 2 ));
alpha = 0.025;
Vratio = 0.39135;
df=2;
Minimize( expression, { df( 2, 1000 ) }, << Use Numeric Deriv( "true" ) );
show(df);
New Window( "Example",
Graph Box(xscale(-1,26),yscale(-10,0),
Pen Color( "red" );
Y Function( expression, df );
)
);
you can zoom in on the sharp drop and see it is going to be computationally difficult to get a perfect answer:
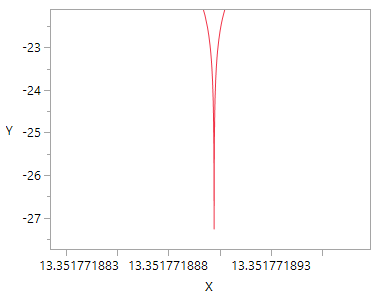
minimize found df = 13.3517718809044;
I'd guess that the minimize algorithm hits a point on the curve that finds the next point on the far side of the true minimum, and might even be in a cycle bouncing across the minimum. With a different starting value, it might get close enough to decide to stop. Close enough is also a parameter you can pass to minimize (tolerance).
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us