- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Is it possible to have one factor which is not significant in a response surface...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Is it possible to have one factor which is not significant in a response surface model but the quadratic term for the same factor is?
I'm trying to model one of my responses in JMP which has been evaluated using a DoE CCD design. In the DoE model, I have one factor which is not significant to the model around this response (p >0.05) but the quadratic term is significant (p<0.05). According to the Effect Hereditary Principle, in order for an interaction to be significant, at least one of its parent factors should be significant. Does this also apply for quadratic terms? How should this be interpreted?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Is it possible to have one factor which is not significant in a response surface model but the quadratic term for the same factor is?
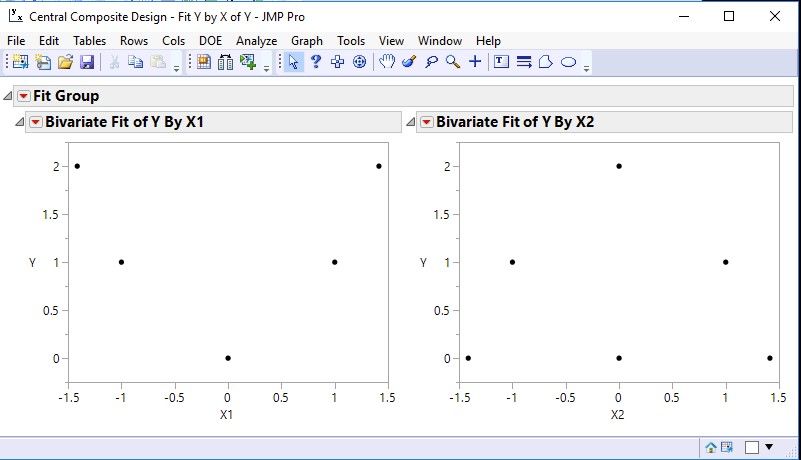
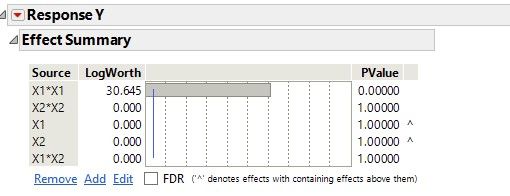
Effect heredity is a guideline/concept/principle, not a hard and fast rule. It's a principle to help guide us in how we may choose to characterize systems with linear in the parameters models. So it's entirely possible for a main effect to not be significant but a quadratic effect for the same factor is significant. Here's a simulated example. Note the perfectly symmetric parabola for X1. And the resultant Fit Model analysis showing only the X1*X1 term is significant. And without being entirely pedantic, when we use the word 'factor' we generally mean the physical 'thing' that is in a system. When we talk about 'effects' we talk about various ways in which a factor can be included in a linear/nonlinear for that matter model. So to say a 'factor' is NOT significant, I would interpret that as ALL the effects including that factor are not significant. But to say an 'effect' is not significant means a specific single term in the model is not significant. So in the situation below, the X1 factor is 'active', but the X1 main effect is not significant, but the X1*X1 effect is significant.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Is it possible to have one factor which is not significant in a response surface model but the quadratic term for the same factor is?
Effect heredity is a guideline/concept/principle, not a hard and fast rule. It's a principle to help guide us in how we may choose to characterize systems with linear in the parameters models. So it's entirely possible for a main effect to not be significant but a quadratic effect for the same factor is significant. Here's a simulated example. Note the perfectly symmetric parabola for X1. And the resultant Fit Model analysis showing only the X1*X1 term is significant. And without being entirely pedantic, when we use the word 'factor' we generally mean the physical 'thing' that is in a system. When we talk about 'effects' we talk about various ways in which a factor can be included in a linear/nonlinear for that matter model. So to say a 'factor' is NOT significant, I would interpret that as ALL the effects including that factor are not significant. But to say an 'effect' is not significant means a specific single term in the model is not significant. So in the situation below, the X1 factor is 'active', but the X1 main effect is not significant, but the X1*X1 effect is significant.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Is it possible to have one factor which is not significant in a response surface model but the quadratic term for the same factor is?
Adding to @P_Bartell, this situation brings up the topic of 'model hierarchy.' The presence of the squared term causes a hierarchy. X is present in X*X. As such, it is strongly recommended that you maintain the hierarchy. That is to say, If the X*X term is significant but the X term is not significant, keep both terms in the model.
JMP checks for such cases and warns you if removing a term will affect the hierarchy. JMP will allow you to proceed, but it is not recommended.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Is it possible to have one factor which is not significant in a response surface model but the quadratic term for the same factor is?
Mark is correct as this is effect hierarchy. Think of it this way, if you are going to "model" the curvature of the factor (X*X) then you will certainly need to manage X. Whether it contributes to the prediction precision or not is really of little consequence.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us