Interpretation of a Factorial Design with binary outcome

[#1]

Hello!

I am struggling with interpretation of factorial design with 4 elements. Before I tried experiments with 2 elements, and results were straightforward.

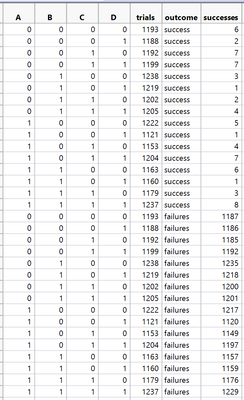
Here in the attachment you can see my jmp dataset file with the experiment.

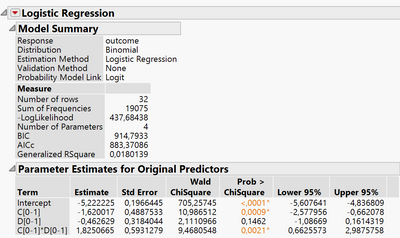
As a result of removing non-significant elements I came to a conclusion that only C and В are significant with negative effect.
Is my conclusion correct?
Rsquare value is very low however chisquare value for elements is significant.
Maybe the experiment is underpowered and needs bigger sample size? 

PS.
Sorry for newbie questions, I am still learning.  
In general, trying to interpret different DoE experiments when I reduce the degree of factorial design from full to a degree of 2 or remove some variables from a model the effect of the same variable changes significantly sometimes to an opposite direction. 
Do I need to look at misinterpretation rate to choose a model in this case?
Are obliged then to run a follow-up experiment with the winning variable, or you can just ship it? What is the approach here?
Can you please point me to an article or a book with a structured approach how to interpret results of binary DoE?

Thanks

[#2]

First of all, binary responses often lead to very low R square even when there are significant relationships. It just means that there is a large uncertainty in the predicted outcome for given conditions. It might be due to lack of fit, but again, it is very common with such a response.

[#3]

Third time is a charm?

The probit analysis worked but the results are practically the same.

Also, there is nothing wrong with your data - my bad.

Part of the reason for the low R square is that you have a rare outcome (success proportions) and the counts are not very different as the conditions change.

[#4]

Perhaps Mark is right on the Probit analysis. I am not sure. I also see that Mark saw some data issues which need to be resolved.

What I noticed is that the probability of a success is EXTREMELY low. The highest probability of a success for any experimental condition is 0.006. This causes a problem because I don't even need to consider your factors. If I always predict a failure, I will be correct at LEAST 99.4% of the time. That's a very good model. It is not very informative, but it is good. This will cause issues for any modeling approach.

I think you should correct the data issues and rethink the analysis approach and what information you are looking for from the analysis. Best of luck.

[#5]

Thank you for your reply!
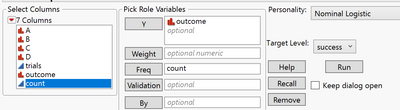
Sorry I mistakenly named successes column, it should have a name of count. If I understood your question correctly.

So is it better to use Nominal Logistic regression to define significant variables and binomial GLM for interpreting their effect size?
Regarding power analysis, in this case if we have only 2 levels then we can calculate sample size as if it was a OFAT (A/B experiment), which would yield to 80K trials in total if we want to detect an effect of 20% with current success rate of control. This is more than I have in the dataset (20K). So maybe bigger sample size is required.

What conclusions would you make based on these results?

[#6]

I think that either logistic regression or binomial GLM can be used for deciding about significant effects and interpreting the nature of these effects.

The power analysis platforms under DOE > Design Diagnostics > Power and Sample Size are not the best tools for multiple factor experiments. These power analysis tools are not appropriate when there is more than one factor because the results are over optimistic since they do not account for the amount of the sample required to estimate and test the other effects.

I generally recommend using the Design Evaluation > Power Analysis tool available within each design platform. You can read more about this feature here. But note that this tool assumes a continuous response. And the separate power analysis tools for a binary response do not adapt to more than one factor. You would have to assume the result is best case and build in a margin somehow.

[#7]

Thank you! I will try it out.

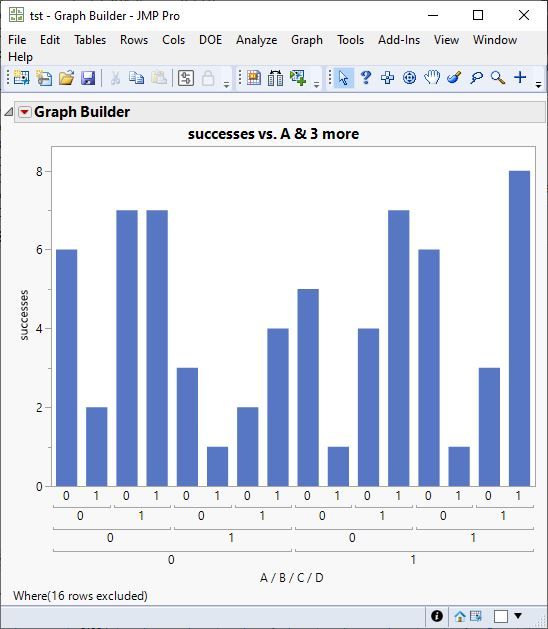
I know that if there is a significant interaction effect then we should include it in a model even though one of the main effects may not be significant. As it is the case. But how can we interpret the fact that when С at 0 level and D at 1 - we have a decrease in success rate by 50% while В is not significant.
However, when С and D both at level 1 they increase success level by 20%.

[#8]

What does you knowledge of the process in question tell you over and above p values and other statistical measures? Process knowledge takes precedence over statistics...if the interactions make sense from a physical understanding of the system...then unless some nuisance or noise variable jumped up and bit the experiment...go with your knowledge.

Perhaps you can share the actual experiment and response data along with your analysis? We might be able to offer other thoughts.

Oh never mind...I just saw that you actually shared the experiment and analysis with us.

[#9]

Your case, change C from 0 to 1 while holding D at 1 is not an example of an interaction. It is just the conditional effect of changing C.