- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How to select independent variables via PCA?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How to select independent variables via PCA?
Hi all,
in order to develop a prediction model I have the need to accurately filter the variables to use. Specifically, I want to use variables that are not correlated. One effective way of doing this is to apply PCA and select the variables providing an eigenvalue > 1.0. If I apply this example to the JMP example (Principal Components Report), then I would select only 1 variable. In my data, the number of variables with an eigenvalue > 1.0 are 9. Therefore, I know with no doubts, how many variables I want. What is unclear to me is how to identify those variables in the JMP report. If, again, I use the JMP example (Principal Components Report), how do I identify the variable (among the six) providing an Egeinvalue of 4.7850?
Thanks,
David
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to select independent variables via PCA?
David,
Are you looking for the eigenvectors? They are available in JMP (under the red triangle). Remember that PCA is a "dimension reduction" technique with each PC being a combination of all variables.
Peter does make good points about using alternative methods for variable selection.
Karen
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to select independent variables via PCA?
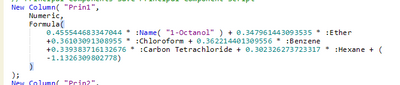
If you use the hotbutton, you should be able to "Save Principal Components" to the data table. Then they'll just be named Prin1, Prin2, Prin3, etc...
The value is not truly corresponding to 1 of the six variables. It's a formula that looks like this:
.
I'm not sure this is exactly what you were asking but I hope it helps.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to select independent variables via PCA?
Unfortunately it is not what I'm looking for. Suppose that in the example I need to identify, among the 6 variables, the 3 least (cross) correlated variables. Which are they? Chloroform, Benzene and Hexane?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to select independent variables via PCA?
You're probably losing a decent amount of information from this method, but this should be able to pull out the 3 materials with the "least correlation" to one another. They won't be orthogonal for sure. There's probably a better way to frame this (something like what Peter is saying) in order to get the answers you want.
*Caveat, this is purely made up and I don't know how sound it is. It makes sense in my head that it does what I think you're asking for though"
dt = Open("$Sample_DATA\Solubility.jmp");
//do multivariate across all the chemicals
mv = Multivariate(
Y(
:Name( "1-Octanol" ),
:Ether,
:Chloroform,
:Benzene,
:Carbon Tetrachloride,
:Hexane
),
Estimation Method( "Row-wise" ),
Matrix Format( "Square" ),
Scatterplot Matrix(
Density Ellipses( 1 ),
Shaded Ellipses( 0 ),
Ellipse Color( 3 )
)
);
mv_r = mv << report;
//make the correlations into a data table
dt_corr = mv_r[MatrixBox(1)]<<Make into Data table();
//sum up correlations for all
dt_corr << New Column("Total Correlation", Formula(
Sum(
:Name( "1-Octanol" ),
:Ether,
:Chloroform,
:Benzene,
:Carbon Tetrachloride,
:Hexane
)
));
//the lowest three are the "least correlated" to one another
materials = :Row << Get Values;
mat = :TotalCorrelation << Get Values;
top = sortascending(mat)[3]; //picks the value for 3rd lowest
what_you_want_maybe = materials[loc(mat<=top)] //grabs the 3 lowest Total Correlation chemicals
Returns:
{"1-Octanol", "Ether", "Chloroform"}
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to select independent variables via PCA?
David:
Since your focus is on ultimately building a predictive model, rather than use PCA on the independent variables as a variable selection tool for finding the uncorrelated independent variables, then I'm presuming you'd focus on using ordinary least squares, with maybe a stepwise approach thrown in, have you considered using a more direct predictive modeling approach that leverages the correlation/covariance structure among the independent variables to give you a useful model?
What I'm afraid is if you just use the uncorrelated variables you may be throwing some predictive power out the window without really knowing it. Partial Least Squares and, if you have JMP Pro, the penalized regression procedures in the Fit Model -> Generalized Regression personality are tailor made for the predictive modeling scenario where correlation among the independent variables is suspect or evident. Two of the techniques, Lasso and Elastic Net have a variable selection aspect to their use. Here's a couple links to the JMP online documentation to these two platforms:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to select independent variables via PCA?
Hi Peter,
your approach assumes the use of a specific prediction model. My approach would be in filtering the variables to use via PCA, and then using a large spectrum of prediction models. As such, the filtering (i.e., PCA) should be independent from the prediction model in use.
From your answer I can tell you are an expert here. Because you have not been able to answer my question in a direct way I will deduct JMP is unable to report the list of variables "linked" to the eigenvalues.
Thanks anyway,
David
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to select independent variables via PCA?
David,
Are you looking for the eigenvectors? They are available in JMP (under the red triangle). Remember that PCA is a "dimension reduction" technique with each PC being a combination of all variables.
Peter does make good points about using alternative methods for variable selection.
Karen
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to select independent variables via PCA?
Yes, you are right.
I was thinking I was able to select a set of attributes among the original ones whereas with PCA I can create new ones (by using the original ones).
The topic is closed. Thanks a lot for the support!
Davide
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us