- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How does JMP adjust for p-value of Pearson Chi-Squared Value
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How does JMP adjust for p-value of Pearson Chi-Squared Value
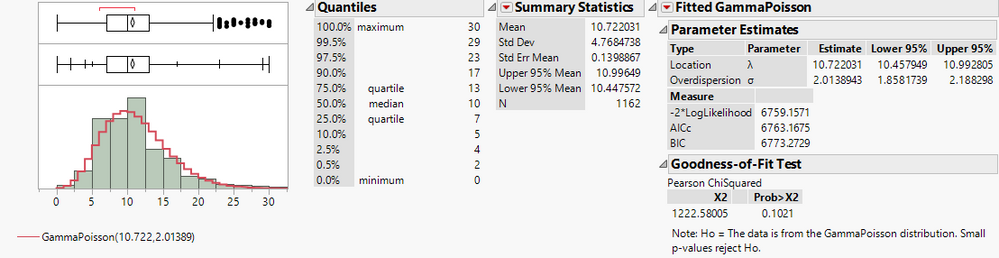
I'm doing a discrete fit between an observed count distribution and a Gamma-Poisson mixture. However the Pearson Chi-Squared Goodness-of-fit statistics is returning a very high value for X2, but indicating an acceptable p-value.
In the example provided, X2 is 1222.58, which if inserted into a Chi Squared distribution would return a p-value of 7.552193e-268.
JMP returns a p-value of 0.1021.
Is there some adjustment that is done in JMP's calculation that would increase the value so much over a direct calculation?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How does JMP adjust for p-value of Pearson Chi-Squared Value
The expected Chi Square under the null hypothesis is equal to the degrees of freedom. Your degrees of freedom are high for this example, you have an N of 1162. Therefore I am not surprised by the results.
Most issues with the Pearson Goodness of Fit tests comes from the bin sizes.
The Pearson Goodness of Fit test has changed for Version 15. The problem with this test is that the bin size it not well defined. For version 15, JMP makes sure there are at least 5 expected observations in each bin. This way we satisfy that rule of thumb (the assumptions are towards the bottom). https://en.wikipedia.org/wiki/Pearson%27s_chi-squared_test
The last bin is the exception. If it's expected count is less than 5, JMP does not worry about it.
Previously, JMP treated every integer between the min and max as a bin. This means there can be bins with zero observations and expections essentially zero.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How does JMP adjust for p-value of Pearson Chi-Squared Value
The expected Chi Square under the null hypothesis is equal to the degrees of freedom. Your degrees of freedom are high for this example, you have an N of 1162. Therefore I am not surprised by the results.
Most issues with the Pearson Goodness of Fit tests comes from the bin sizes.
The Pearson Goodness of Fit test has changed for Version 15. The problem with this test is that the bin size it not well defined. For version 15, JMP makes sure there are at least 5 expected observations in each bin. This way we satisfy that rule of thumb (the assumptions are towards the bottom). https://en.wikipedia.org/wiki/Pearson%27s_chi-squared_test
The last bin is the exception. If it's expected count is less than 5, JMP does not worry about it.
Previously, JMP treated every integer between the min and max as a bin. This means there can be bins with zero observations and expections essentially zero.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How does JMP adjust for p-value of Pearson Chi-Squared Value
Thanks Tonya, that helps a lot. Is there a way to control the bin size for ver. 15 and above? In the example I have provided, I believe I wasn't giving the correct degrees of freedom for the Chi Squared Test in the alternate methods I was using.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How does JMP adjust for p-value of Pearson Chi-Squared Value
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us