- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Don't understand difference between Number of runs and replications
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Don't understand difference between Number of runs and replications
Hello,
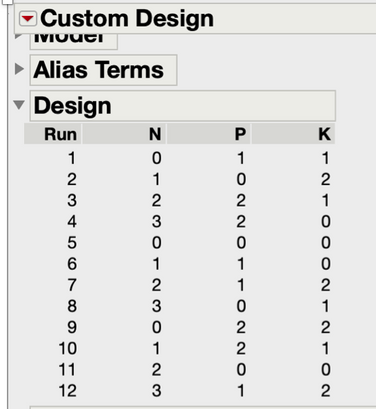
I am trying to design a sugarcane fertilization experiment with 4 levels of nitrogen, 3 levels of phosphorus, and 3 levels of potassium in a fractional factorial design. I got this design with 12 runs :
Can I use only 12 plots (= to 12 runs) or should use replications (3 or 4 replications) of the 12 runs ? Thank you for your help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Don't understand difference between Number of runs and replications
The custom design guarantees that the parameters in your model are estimable. So the 12 runs are a sufficient number of runs. The matter of the number of runs affects the standard errors of these estimates by increasing sample size and potentially decreasing (eliminating?) correlations.
If you specify a larger number of runs (e.g., 24), then custom design will use the bigger budget optimally. If you force JMP to replicate runs (2x12) to achieve the same number of runs, the design might not be as good. In other words, the design that you get by asking for n runs will not be same same design that you get if you replicate a runs b times such that axb = n runs and a minimum amount of replication.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Don't understand difference between Number of runs and replications
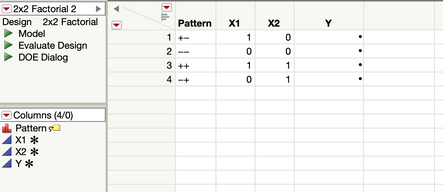
Thank you for your reply. But when I design a complete factorial design for example for 2 factors at 2 levels, I get 4 plots, which is one replication as shown here :
In the field, I have to run 3 or 4 replications of the 4 plots in order to account for experimental errors. That's why I am wondering if the 12 runs in my design represent 1 replication.
##- Please type your reply above this line -##
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Don't understand difference between Number of runs and replications
A full factorial design for a 4-level factor and two 3-level factors contains 24 unique treatments. So your design with 12 runs is a half fractional factorial design.
You can use the DOE > Classical > Full Factorial Design, the enter the number of desired replicates. The design (24 runs) counts as 1 replicate. If you enter 1 for the number of replicates, you get another one for a total of 2 replicates (48 runs).
You can use DOE > Custom Design. Just enter the total number of runs (e.g., 48 runs for 2 replicates) to include all the replicates that you want. The custom design will produce the optimal design, which will be the full factorial design in this case.
So you should be able to get the (4x3x3) x Replicates either way.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Don't understand difference between Number of runs and replications
My math might be wrong, but a full factorial for 4^1 x 3^2 = 36 treatments (runs). Replication, or Blocking is used to determine if the results from one replicate repeat over changing noise. The purpose of Blocking is to reduce the amount of noise changing within the Block by holding the noise constant or sampling such that the noise does not change much within the replicate. For an agricultural example, run all of the treatments in a small area of the field over a short time period reducing inherent soil fertility and ambient condition changes thereby increasing the precision of the design. When subsequent Blocks are run, the noise that was constant during the first set of replicates, changes (either by manipulation or sampling). For agricultural example, run the second set of replicates at another location in the field and under different ambient conditions. If you use hypotheses about the effects of noise, you can more efficiently select what noise to study by Blocking.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Don't understand difference between Number of runs and replications
@moughli, I had some other thoughts about your situation if you'll indulge me. I'm not sure why you are running experiments on factors at more than 2 levels if you are wanting a fractional factorial. You are likely to confound higher order linear effects (2nd+ order interactions) with non-linear effects (quadratic and cubic).
Some thoughts:
1. Perhaps you should think of the factors as ratios of each component (if indeed you need all components in the final solution),
2. You might want to think about a mixture design, but only after you have identified, studied and understand the noise,
3. Seems there is likely interaction between the factors and the noise (amount of each ingredient depends on the current soil conditions), so it is paramount that you understand these before optimizing the levels of the controllable factors.
4. I might suggest understanding the first order model for the factors of interest (2 level designs are adequate for this) and identifying noise-by-factor interactions before proceeding with response surface type designs.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us