- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Distribution platform
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Distribution platform
Hello,
Need some advice.
I used distribution platform to check best fit for my data. I wanted to know, if there is any way to check what is the level of error (in central tendency and variance) introduced if we assume a non-normal distribution as a normal distribution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distribution platform
Hi @billi,
I understand that you want to understand the "level of error" from assuming that data have a normal distribution when they really come from a non-normal distribution. Is that correct? That is an interesting question.
Can I ask why you want to do that? Do you have a real situation where you need to do this that you can tell us about?
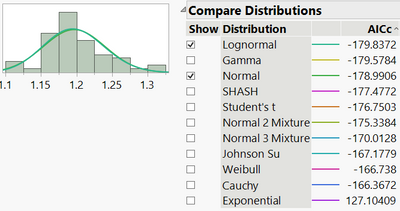
I am not sure how the data were generated in your example - maybe this is from a real process? But your Compare Distributions analysis suggests that the log-normal distribution might be the best distribution.
Having said that, the Gamma and Normal distributions have a similar AICc. AICc is a measure of goodness-of-fit and we generally say that a difference in AICc of less than 2 is not significant.
So that would suggest that, in this case, that the "level of error" in location/scale/central tendency and dispersion/shape/variance will be small from assuming a normal distribution if the distribution is really log-normal. You can see this from the fitted distributions on the plot - they are almost indistinguishable (especially as they are a similar colour!).
Does that help? Do you have a particular way that you might want to quantify "level of error"? How do you know what is the "correct" distribution in order to then look at the error from assuming an "incorrect" normal distribution?
Phil
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distribution platform
Thank you @Phil_Kay for the response. I agree with you there is not much difference between the lognormal and normal here. But I do have another data in which difference is about 5 AICc but I'll check the quantile profiler with that and if something comes up I'll post it. Thank you very much again for your help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distribution platform
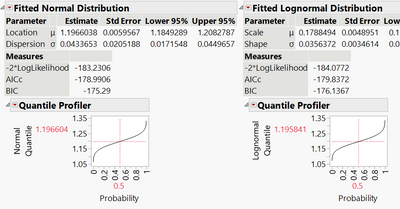
Another idea that you might find useful is the Quantile Profiler from the red triangle menu for each fitted distribution. You can use these to compare quantiles. Below you can see the median (Probability = 0.5) and the 10th percentile (Probability = 0.1) estimate for each distribution. Again, this is showing negligible differences between the distributions.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us