DOE Mixtures with disallowed combinations of components

[#1]

Hi,

I have read one of the documents in the site (7 Component Mixture Design with Additional Constraints)

I have a similar problem; I have one mixture component (A) for which i have three different types (A1, A2 and A3). I have similar constraints to what include in your paper (min/max % of A as a whole). However i also want to evaluate mixtures with 

* only A1 or A2 or A3 within total limits min/max for A

* a combination of A1+A2 or A1+A3 or A2+A3 within total min/max for A

Is there a way to put these constraints in JMP? I have found that the disallowed combination filter does not work for continous mixture factors so i dont really know how to do this.

I suppose a way around is to do 3 different designs (A1+A2) and (A1+A3) and  (A2+A3) but i was wondering if there a way to do only 1 design with those constraints.

Any suggestions?

[#2]

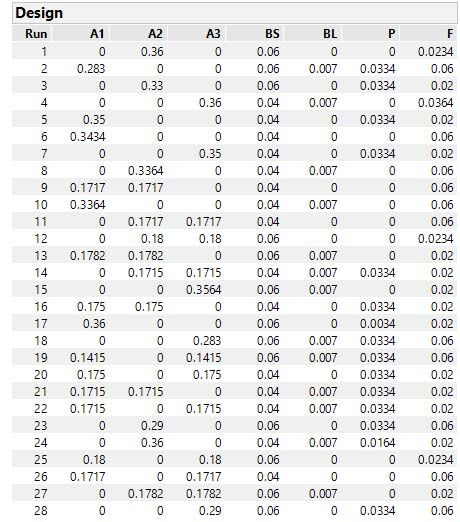
I think the key to getting two of the As in the trials is including in the model the 3 interaction terms among the As.  

Here's my resulting design with the 10 term (vs. 7 term) model showing lots of pairwise combinations and no three-way combinations of As.

I hope this delevers what you want.  Thanks for the good discussion.

[#3]

Hi Tom,

Thank you again for your reply.

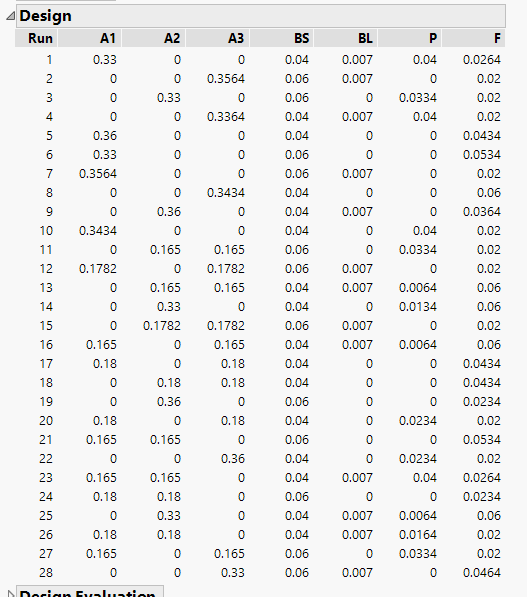
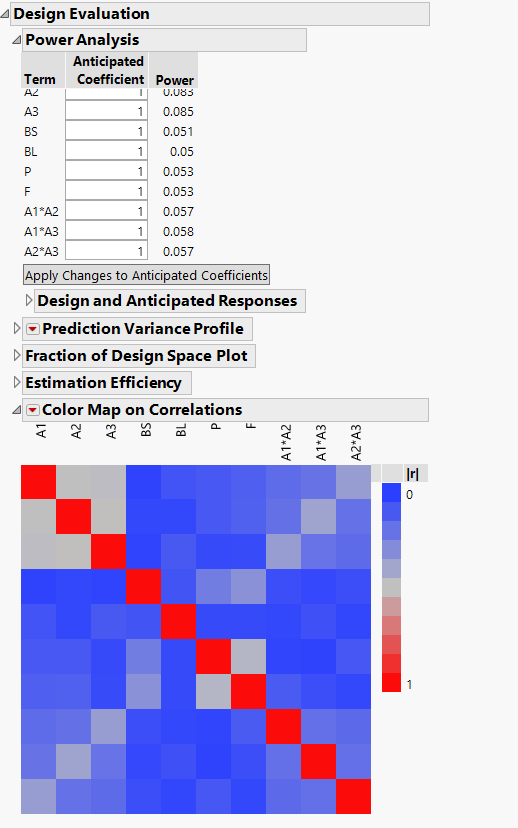
I did include the interaction between the A components and I get something similar to your design. I attach the views below.

Would you say that this is a good "design" or do you think as well that we should make more effort to enlarge the ranges for the factors to have a more robust experimental program?

Thanks

asier

[#4]

Asier,

Happy to see you can produce a similar design satisfying the desire to have binary blends of the As.

As for is it a good design?  You never stated and I never asked what is(are) your goal(s)?  If it is to be able to optimize the process, then why not include all interactions to make a potentially more predictive model?  If it is to do screening to find out better performing levels or whether a component makes any difference over the proposed ranges, then I would say "yes, it is good."  As you have already discussed with Mark, expanding ranges (being bold) helps to increase the size of the effect relative to the noise in the process and therefore increases power.  Good luck experimenting.

Tom

[#5]

Hi Tom,
Thank again for your reply.
I think the final objective would be to optimize the process (however, my colleague for the time being is not asking for that, just for "an experimental program to evaluate some improvements". This is probably one of the reason of the small ranges for the factors (because they already have an idea of "what" the want to replace and by "how much"... although they don't really know the impact on performance.
>From the factors, they want to see if they can replace some of A1 by A2 or A3 (or potentially even a A2+A3 mixture). Then, they also want to see if they can replace some of FL by FS. And also see if we can decrease the content of P and F. I would say this is more optimization than screening (Would you agree? Although a good outcome may be that A2 or A3 are not as good as A1 (which would be more screening that optimization then?).
I did not put all the interactions from the beginning because when I did, I was getting very few runs with only two A components (8 out of 56 runs). So, I thought that this was defeating my purpose. However, I was also thinking that for a proper optimization I would need the interactions between all factors.... And that is why I was trying to see if we can define these constraint somehow into the problem.
The reply from Cameron could be a potential solution for the constraint (only 2 A's). However, I am not sure of the mathematical implications of such a solution (I will not be able to fill directly the "runs table" with the results and somehow I am not sure how I will have to fill in the results and interpretate the results... what do you think?
Then, I am still curious about the implications of the little variation of the factors (the low power, etc) and getting little "value" from the experiments... so that is why I wonder how we can improve the design (if possible).
Thanks again!

[#6]

Hi Mark,
Thank you for your reply.
I am doing this design for a colleague with no experience in DOE. I was suspecting as well that the experimental ranges are too small and I passed that comment already to "question" the reasons for that. I have to wait to see if the ranges for the factors can be increased
My first concern was about how accurately we can control the weight of the ingredients within such a small range, and secondly about the real effect (and the measurement) of changing some factors by so little.
I see from your reply that we also have mathematical consequences from the slow ranges and the linear constraints. Thanks you for the information!
Asier

[#7]

I often find that experimenters limit factor ranges for no good reason. The choice is guided by what they think they know and not by the requirements of the regression analysis ahead. "I think that the best level is 12% so I will test 10% to 15%." Not a good idea. That idea comes from a testing mentality, not an experimenting mentality. The range should always be as wide as is realistically possible in order to produce the largest effects. (I am fully aware that there are often physical limitations on the ranges. That limitation is not what I am talking about.) That way will maximize power (without necessarilky increasing the number of runs), minimize the relative standard error of parameter estimates and predicted response, and narrow the confidence intervals. Most informative.

Why narrow factor ranges? Why not widen them? This lesson is stubbornly ignored. It is a mentality thing.

(Note that this is my personal opinion.)

[#8]

Hi Mark,
I agree. I think in this case the limitations from the factors are just coming from what you said (I want 12% and I will test between 10% and 15%). That is what I told my colleague already (let’s hope we can move away from that) 😊
At the same time, the Power concept is not really clear to me… so I cannot really “reason” this topic well with her…. if you can elaborate further on that (or give a good starting reference on your website, I think some people will find it useful). I had a look at a video from Tom and that helped already (and probably after a few “encounters” with this topic, it will become clearer… if you have a good basic reference (with some examples, please!) you will make my weekend!
Thanks again

[#9]

Power is the probability that you will decide that a real effect is significant or that you won't make a type II error. That is, the alternative hypothesis is true (there is a real effect). For example, in a regression analysis such as the one used to fit the linear model to the experimental data, the null hypothesis is that a parameter is 0 (no effect). The alternative hypothesis is that a parameter is not 0. We could use a t-test to decide. The t-ratio is the (estimate - hypothesized value) / (standard error of the estimate). By widening the factor range, you produce a larger effect (and a larger estimate). That change, in turn, produces a larger numerator in the t-ratio. A larger t-ratio will have a smaller p-value. You are more likely to decide that the real effect is significant.

On the other hand, if you arbitrarily narrow the factor range, the change is in the opposite direction. You will produce a smaller effect that leads to a smaller numerator and, therefore, a smaller t-ratio with a higher p-value. Now it is more likely that the decision will be that the effect is not significant.

Caution: even if you can get them to widen the range now, once they know where the factor should be set, the mentality will return and they will want to narrow the range when this factor is in a future experiment. You never narrow the factor range.