Hello,
I am still new to JMP but I'm trying to determine the best way to model a non-linear system (generating DOE + model fitting).
Context: Long story short, I have a large experimental space that I am trying to model (10 discrete variables + 10 continuous variables). Before I jump into my full experiment I'm working with a subset (1 discrete variable + 5 continuous variables) to make sure I'm modeling my system correctly before expanding my experimental space.
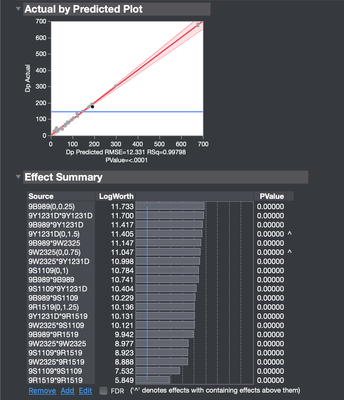
I started by generating a DOE with a simple model containing main + 2nd Interaction terms + 2nd Power terms. After running the DOE I have a model that fit nicely where all effects are significant.
As I play with the `Prediction Profiler` I know my model is over fitting certain sections of the data which are causing predictions that are not physically possible. My goal is to make a model that's as accurate as possible over my entire experimental space. Please see my screen shots below explaining some edge cases that are not being modeled accurately:

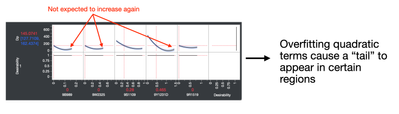

Summary of where I currently stand:
- I know there is statistically significant curvature in my response (based on my first DOE)
- I know from physics that the response should asymptotically approach 0 as my continuous variables go to infinity (impossible for response to be negative)
- There are possibly some interaction terms but I'm wondering if those terms are also being used to overfit the curvature in my response. I need a bit more evidence before I believe there are significant interaction terms.
My current model is accurate in 90% of scenarios, but I know there are some edge cases being generated because quadratic terms can't accurately model an asymptotic response. I assume that if I added more data points near the minima in the quadratic region the model would smooth out and more closely match reality but I want to minimize the number of data points required to get a good model (especially before I add more variables). What is the correct way to generate a DOE for an asymptotic response and once the DOE is generated, how do you model this non-linear response properly?
Thanks!