- Due to inclement weather, JMP support response times may be slower than usual during the week of January 26.
To submit a request for support, please send email to support@jmp.com.
We appreciate your patience at this time. - Register to see how to import and prepare Excel data on Jan. 30 from 2 to 3 p.m. ET.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Comparing means using different methods give different results
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Comparing means using different methods give different results
Hi all,
I have a quick question about comparing means in JMP 15. My data is composed of two variable:
the independent variable is an ordinal variable with four levels (high, medium, low and very low), while the dependent variable is continuous.
I want to compare means for four groups (high, medium, low, and very low) to see if there is a statistical difference between them or not. when I used (All pairs Tukey-Cramer method) , no statistical difference was found between all means. However, when I used (Each pair student's t method), a statistical difference between the "very low" and the "high" levels was found.
My question is:
1- why there is a differences between the two methods?
2- which one should be used?
Thank you in advance,
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Comparing means using different methods give different results
I believe this is covered in the documentation, but briefly the compare each pair pretends that the only data you have is each pair that is being compared (i.e., it is equivalent to subsetting each pair of groups and testing for a difference, in isolation). The Tukey HSD takes into account that you are making multiple comparisons and ensures that the probability of a type 1 error reflects the totality of the tests for differences between pairs. So, if you were doing 100 tests (many groups to compare), there is a sizeable chance that even if you find p<.05 in each of the pairwise tests, that some of these will produce type 1 errors. Tukey is much more restrictive (and more so, the more groups you have) in that each pairwise test is subject to much greater scrutiny to ensure that your overall probability of a type 1 error covers all of the tests you will be conducting.
The pairwise comparison is almost certainly too lax. But with many groups, I have found Tukey to be perhaps too restrictive. It is worth doing both - and when the results differ qualitatively, be humble about your conclusions (at least more humble than if the two approaches give the same qualitative conclusions).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Comparing means using different methods give different results
Hi @IceBreaker ,
as @dale_lehman explained, Tukey controls for multiple comparisons by maintaining an overall Type one error at 5%. In addition, it assumes equal variances across the groups.
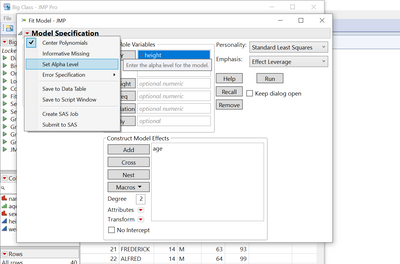
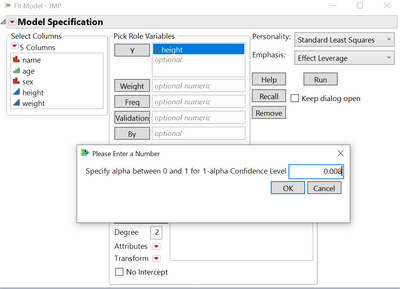
in this situation i would perform the comparison test once again using the Bonferroni correction. To do this divide 5% (or whatever type I error you want to allow for) by the number of pairwise comparisons you have (6 for 4 different categories). Before running the model, in the red triangle of the fit model platform set the alpha level to that new value (0.008). Then perform the t test multiple comparisons and inspect the results once more.
Most important, I suggest you inspect the pairwise comparisons table and ask yourself for each significant pair whether it is also meaningfully different - are the group means you have different in the real world. IF you saw two observations with the two different values would you be able to say that they are substantially different and considering them to be indifferent doesn't serve the purpose of the study. I find it striking how so many people do not make sure this is the case when reporting significance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Comparing means using different methods give different results
I believe this is covered in the documentation, but briefly the compare each pair pretends that the only data you have is each pair that is being compared (i.e., it is equivalent to subsetting each pair of groups and testing for a difference, in isolation). The Tukey HSD takes into account that you are making multiple comparisons and ensures that the probability of a type 1 error reflects the totality of the tests for differences between pairs. So, if you were doing 100 tests (many groups to compare), there is a sizeable chance that even if you find p<.05 in each of the pairwise tests, that some of these will produce type 1 errors. Tukey is much more restrictive (and more so, the more groups you have) in that each pairwise test is subject to much greater scrutiny to ensure that your overall probability of a type 1 error covers all of the tests you will be conducting.
The pairwise comparison is almost certainly too lax. But with many groups, I have found Tukey to be perhaps too restrictive. It is worth doing both - and when the results differ qualitatively, be humble about your conclusions (at least more humble than if the two approaches give the same qualitative conclusions).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Comparing means using different methods give different results
Thanks @dale_lehman for you detailed response.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Comparing means using different methods give different results
Hi @IceBreaker ,
as @dale_lehman explained, Tukey controls for multiple comparisons by maintaining an overall Type one error at 5%. In addition, it assumes equal variances across the groups.
in this situation i would perform the comparison test once again using the Bonferroni correction. To do this divide 5% (or whatever type I error you want to allow for) by the number of pairwise comparisons you have (6 for 4 different categories). Before running the model, in the red triangle of the fit model platform set the alpha level to that new value (0.008). Then perform the t test multiple comparisons and inspect the results once more.
Most important, I suggest you inspect the pairwise comparisons table and ask yourself for each significant pair whether it is also meaningfully different - are the group means you have different in the real world. IF you saw two observations with the two different values would you be able to say that they are substantially different and considering them to be indifferent doesn't serve the purpose of the study. I find it striking how so many people do not make sure this is the case when reporting significance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Comparing means using different methods give different results
Hi @iron_horne,
Thanks for your feedback,
I have done the Bonferroni correction as you explained. but I do not understand what do you mean by perform the t test multiple comparisons? is that All Pairs, Tukey HSD?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Comparing means using different methods give different results
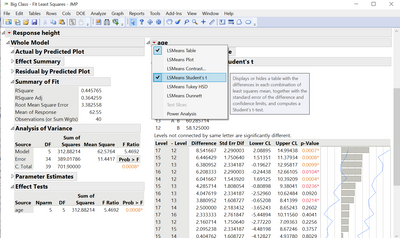
i mean ask for the student's t test and its ordered differences report. As in the following images.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us