Hi @SerialDeviation : It might help to put the problem in the framework of hypotheses testing.
Suppose p1 is the failure rate for the old part, and p2 is the failure rate for the new part.
Do you want to "prove" p2-p1<0.10? (i.e., and absolute difference of no more than 10%):
If so, your null and alternative hypotheses are:
H0: p2-p1=0.1.
Ha: p2-p1<0.1.
Then this is indeed an NI study, you have to ask yourself some questions:
(1). Are the failure rates independent? i.e., does part 1 failing influence whether part 2 fails or not (or visa-versa)?
(2). What information do you have about p1 and p2?
(3). What is your desired Type 1 error rate?
Let's suppose the answer to (1 ) is yes (they are independent), and you (2) expect the true proportions to be p1 = 0.1 and p2 = 0.19, and (3) Type 1 error rate (alpha) = 0.05.. Then you can use the "Power Explorer for Two Independent Sample Proportions" as shown below if you want 80% power:
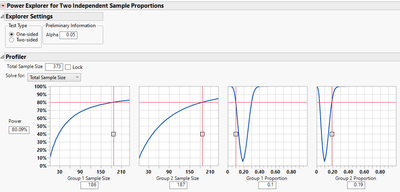
More here: https://www.jmp.com/support/help/en/18.0/index.shtml#page/jmp/power-for-two-independent-sample-propo...
If, however, your alternative (the thing you want to "prove") is:
Ha: p2/p1<1.1 then that is a different animal (that is a relative difference of 10%).