Analysis of DoE model with center points

[#1]

Hello,

I have a d-optimal design with 6 center point experiments. While performing the model building, does JMP take the mean of the 6 center points as a datapoint to fit the model? Or does it take all 6 points as individual points?

What is the correct way to build the model?

In addition, I have one scenario where the variation from the center point replicates is comparable to the variation from the DoE factor variation. In such case, can we conclude that the factors may not be explaining the variation in the response?

Variance from center points= 2.03

Variance from all data points excluding the center points = 2.54

I usually contact @martindemel  for JMP related questions. However, he is away during this week. Hence, posting the question here.

Thank you.

[#2]

Hi @Coverbird30,

There is a lot to unpack in your post and questions.

• Centre points are useful to check for curvature, reduce the prediction error in the center of the factor region and test for lack of fit due to nonlinear effects, but they are not helpful to identify the responsible quadratic effect. No matter the number of centre point, it can only be used to estimate one quadratic effect, so their contribution to model building is very limited. The 6 centre points can't help you estimate several quadratic effects, only give you the opportunity to check for curvature.  
  
  
• Check for curvature is done through Lack of Fit test : it compares the difference between total error (sum of squares calculated on all runs) and pure error (sum of squares calculated on unique runs, so the mean response of your centre points will be used for this calculation). For mmore details about the calculations, you can check 3.8 - The Lack of Fit F-test When There Are Replicates | STAT 462
  
  
• To build a model from a DoE, you start with the assumed model you have specified apriori during DoE creation. From the results of this first model and its adequacy to model the response, you can then iterate and refine the model, depending on your objectives and performance criterion for the model: R²/R² adjusted for explaining the variation, RMSE for evaluating predictive precision, p-values for statistical significance, information criterion like AICc and BIC to evaluate the tradeoff between model complexity and model accuracy (the lower the better), etc...
  
  
• I wouldn't agree with your conclusion regarding the variance calculated in the two conditions. The only conclusion you could have with this situation is that you have an homogeneous response variance over the experimental space, but that doesn't mean your factors do not have an influence ! Let's remember that variance is calculated using a difference from the mean, so for different area, the mean could be different but the difference between values and mean could be the same. For example, having a variance of 2 for a mean of 34 (for centre points) and a variance of 2 for a mean of 68 (for other data point) is clearly not the same situation. I would recommend visualizing the data with graph builder, plotting different Y vs. X graphs to see how each factor (X) may influence the response (Y). You can generalize this plot using Scatterplot Matrix:
  

  You can use these visualization to quickly spot any patterns in your data (like curvature), and already have a first overview about which factor(s) seem to have the most impact on the response.

Try to start simple and iterate: first visualize, then descriptive analysis, then modelization, to benefit from each learning gathered at each step to inform the next one.

Hope the answer will help you,

[#3]

Hello,

Thanks a lot for your reply. It has addressed a lot of my querries. I have one remaining question. In JMP DoE, I got the design from the software. While building the model (All interactions and quadratic effects included) , does the model take the experimental repeats as individual points? Or does it take an average value of the repeats for building the model?

[#4]

Just to be clear, there is a difference between repeats and replicates (yes, words matter).  Repeats are multiple datapoints (e.g., multiple measures of the same experimental unit) while the treatment combination is constant.  Replicates are multiple experimental units for the same treatment combination.  Replicates increase the DF's in the study, repeats do not as they are not independent events.  So do you mean repeats or replicates?

What JMP will do depends on how you set-up the table.  If the repeated data points are in separate rows, JMP will "think" those are independent "events" and will consider them additional DF's.  If you record the repeated data points as separate columns, JMP will "think" those are additional Y's.  You will have to summarize the repeats before doing the analysis of the experiment.  One additional thought is to first determine if it is appropriate to summarize the data points before determining the appropriate statistic.  In other words, are there any unusual data points?  Do the repeats seem consistent within treatment?  If so, then you can calculate the mean and also the variation of the repeated data points.  The variation estimate can be treated as an additional Y.  Therefore you can determine if your model effects impact both the mean AND the variation.

[#5]

Both, depending on what you're looking at in the model :

• For the estimation of terms coefficient in the model, the average value of the replicates is used to calculate them (like an ANOVA would do). This enable to have a more precise estimation of effect terms in the model.
• The individual points are used for the estimation of the model variance and to estimate the variance of terms coefficients. 

Replication enables the experimenter to obtain an estimate of experimental error, see Key Principles of Experimental Design | Statistics Knowledge Portal | JMP. Replicate experiments are not repeats, even if you can have a similar effect on terms estimation between repeats (conducting the same measurement on the same unit multiple times help reduce measurement error, but not experimental error) and replicates in the model (it will improve the effects estimation), it won't improve statistical significance of terms and of the model or variance reduction, as you need a higher number of degree of freedoms brought by independant experiments (like replicates). 

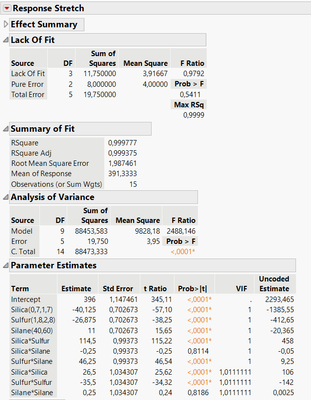
As an example, here is the modeling result from "Bounce Data" in JMP with an unreplicated Box-Behnken design:

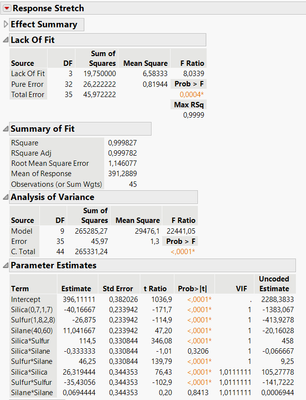
By augmenting the design and adding two replicates of this initial design (so that each runs from the original design is independantly present three times in the augmented design), here are the results:

You can see that parameter estimates haven't changed a lot (I just used similar response values for the replicate runs), but the standard error of each effect estimates has largely decreased (and p-values too) in the augmented version, as well as the error of the model (Root Mean Square Error), thanks to this additional degree of freedom brought by the replicates. 

Hope this answer will help you,

[#6]

As Victor writes, the center points are useful to test the assumption of linearity in the design space.  That estimate is not specific (i.e., A*A = B*B = C*C...).  Since you have 6 , I would start by plotting those in run order.  Any patterns?  When writing the model, you can include one term in the model to estimate the deviation from linear within the design space (a quadratic of any factor in the experiment).  The other DF's will be allocated to estimate the MSE in the design space. If indeed there is more variation in the 6 center point runs, you will likely not see significant factor effects (using p values).