Skeletons and Flying Carpets: A Step Beyond Profiles and Contours to Explore Multiple Response Surfaces
Christian Ritter, Executive Director, Ritter and Danielson Consulting
Abstract
Non-trivial models with multiple input and output variables are hard to visualize, and communication about statistical significance and scientific meaning is far from obvious. Here we are studying the transition from single response displays in which the effects of multiple X variables are shown for a singe Y variable towards two classes of dual response graphs: skeletons and flying carpets and then explore how uncertainty of the model can be integrated.
Keywords
Response surfaces, multivariate analysis.
Motivating Example: Polyurethane Foams
Let us start with a practical example. Polyurethane foams used to make mattresses are the result of a simple chemical reaction. In this chemical reaction, a generalized alcohol called a polyol, reacts with isocyanate to form an elastic polymer. At the same time, water also reacts with isocyanate and forms urea and CO2. The urea disperses in the polymer and hardens it, whereas the CO2 forms bubbles which at some time burst into each other to form a breathable foam. Parameters which define the characteristics of the product include hardness, density, tensile strength, and elongation at break. The first two parameters are related to the general hardness and price class of the foam, the second pair to its elastic properties.
Although, the chemistry is quite simple, there are nevertheless a considerable number of variables which determine the foam characteristics. There is the quantity of isocyanate. It is commonly chosen in slight excess to ensure full reaction. Excess isocyanate then dissolves into the urea domains. Furthermore, the amount of water with respect to polyol at equivalent excess isocyanate will create more gas which makes more and larger bubbles and therefore lower density foam. At the same time, the remaining polymer will be harder since it contains more urea. At the same time, less dense foams have less material to hold up the foam and are in general softer.
Further factors determine the characteristics of the product. Additional solids can be added to harden the foam, auxiliary gas generating materials can further reduce density, flame retardants may be needed to pass safety regulation, and air pressure and humidity affect the outcome. This means that the number of input variables and responses and the complexity of the relationship is sufficiently high to make analyzing the relationship quite tricky.
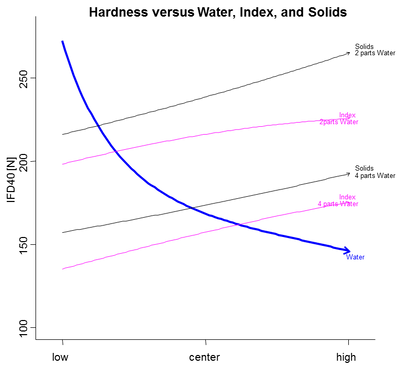
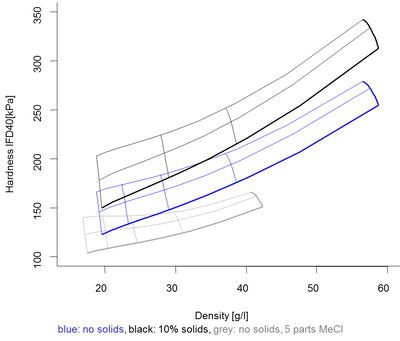
The following graph is an attempt to show how the three most important variables affect the outcome:
Figure 1. Single response graph for IFD hardness of the models presented by R. Schiffauer [1].
This is a single response graph with multiple input variables. Note that the relationships and their relative sizes can be seen for each variable, and one can also compare them. However, no clear summary picture appears. It is also difficult to imagine how to integrate more input variables and how to show interaction effects. Finally, since we wish to understand how the inputs affect multiple responses, several of these graphs have to be studied simultaneously.
Many of us can recall hours of explaining such sets of graphs to the scientists with whom we, statisticians, are collaborating and for whom we have constructed these models.
Skeletons
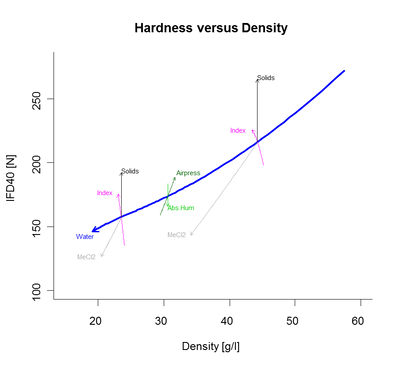
A first alternative is the skeleton plot for two responses as shown in the example below (Figure 2). Here, one first seeks a hierarchy among the X variables. As a backbone, one selects the variable which has the strongest joint effect on both responses. In the example, this is the water content. Then the effects of other variables are grafted onto the backbone. Variables which show little or no interaction with the backbone variable are grafted once, variables which interact with the backbone variable are grafted twice. Higher order interactions can be added as ‘bones’ grafted at a second level (this is not shown here).
As a result, we obtain a display of a very complex situation in a way which remains interpretable to scientists. In the example, the backbone is perfectly logical: As the water level increases, the foam becomes less dense (more gas) and softer (less substance). Yet, more water also means harder polymer. Higher isocyanate excess (index) or additional solids, increase hardness with little or no effect on density and their effects are a bit different at high density foams made with little water (urea) than at low density foams with a high urea content. Auxiliary blowing agents (here MeCl) and air pressure act in logical and opposite ways … We see, main relationships, although complex can be readily explained and in a way which is much easier and clearer than via a pair of single response graphs.
Figure 2. Skeleton graph of IFD hardness and density based on the models published by R. Schiffauer [1].
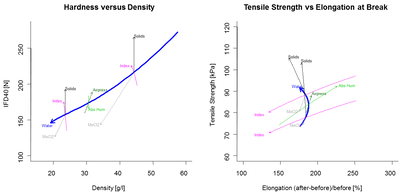
The following pair of graphs show a view of two skeleton plots which allow to explore the four responses simultaneously. This display shows at the same time the strength of the method and identifies one difficulty: The backbone of one skeleton graph may not be ideal for another, made for different pair of responses. Developing methods for choosing this variable automatically still need to be designed.
Figure 3. A pair of skeleton plots for the same input variables.
From Skeletons to Flying Carpets
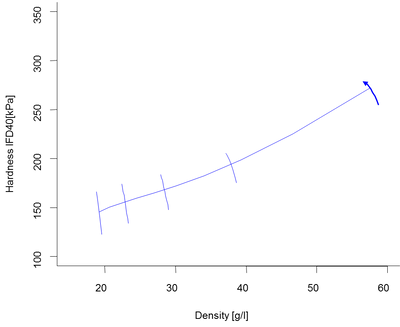
Skeletons help in picturing input output relationships, their sizes, and their interactions. They do not display range of properties which can be attained (under the condition that the model holds). A skeleton lacks flesh. Fleshing out the skeletons means that we have to increase the dimension of the bones to at least 2 and this gets us to flying carpets. A challenge for this display is to identify an anchor point in a visually non-intrusive way.
Figure 4a and b. Fleshing out the backbone representing the water effect by the effect of isocyanate index.
And when there are three input variables, how should we proceed? There are two possibilities: We could go from a two dimensional object (manifold) to a three dimensional one, or we could repeat two dimensional objects. That is, we could go to displays of flying sausages or to multiple flying carpets. The first approach is based on an optical illusion: representing a three dimensional object by showing a visually annotated two dimensional shape. This is very hard to do and also hard to view. The second approach leads to easier displays at the levels of construction and viewing.
Figure 5. Arrangement of Flying Carpets.
And this is about where it ends. Here we show two responses and four input variables to picture the property range in density and hardness which can be covered by the selected formulation range. Skeleton plots can accommodate a few more variables than arrangements of manifolds (flying carpets). In the example, we have six input variables and two responses. These two types of displays are in the following sense optimal: They greatly improve over single response displays by showing more variables and more relationships in a way which is easier to understand. On the other hand, it is not possible to show three responses in a single display since this requires using the illusion of depth. For the same reason, the number of dimensions which can be used in the display object cannot exceed two.
Going beyond two responses requires showing arrangements of two dimensional projections or animation of the graphs.
Ridge Gymnastics
Up to now, we have introduced and discussed skeleton graphs in the case of a known model. In practice, models have to be constructed from data and their parameters are subject to uncertainty. How can one integrate uncertainty with respect to the model and the data?
For this purpose, we shall revisit a complex example reported box Box and Liu [2]. It concerns data collected in the optimization stage in the process of designing paper helicopters which fly when dropped from a bench and whose flight variability is low. There are two responses, flight time in centi-seconds denoted by Y and a measure of variability, 100*log10(stdev(Y)), denoted by LS. There are four input variables, wing area (A), wing length/width ratio (Q), body length (L), and body width (W). The experimental design was a blocked central composite in these four factors.
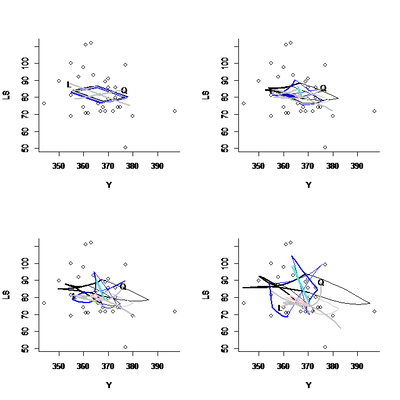
The following set of dual response display (a mix of flying carpets and skeletons) shows a way of displaying raw data and main patterns. The top left graph shows slices made for the two variables which have the largest overall linear effects, body length (L) and wing length/width ratio (Q). We see a tendency for helicopters with higher wing length/width ratio to fly longer at the expense of variability. For the body length, shorter seems better (note that ‘long’ or ‘short’ are with respect to the chosen experimental ranges. When we blend the linear fits with fits of a full model (including interactions and quadratic terms), we see that the slices separate and become quite irregular when only the full model is shown. The full model over-fits and a reasonable fit is probably somewhere in the middle.
Figure 6. Raw data and models. Top left: linear effects only, slices in wing and body length. Top right: mix of 0.8parts linear and 0.2 parts full model. Bottom left: even mix of linear and full model, bottom right: full model.
Bibliographie
[1] Reinhart Schiffauer (1994), Mathematical Property Prediction Models for Flexible Polyurethane Foams, Proceedings of the 35th Annual Polyurethane Technical/Marketing Conference, 225-238.
[2] G. E. P. Box and P. Liu. Statistics as a Catalyst to Learning by Scientific Method Part I – An Example. Journal of Quality Technology, 31(1):1-15, 1999.
Christian Ritter, Executive Director, Ritter and Danielson Consulting
Abstract
Non-trivial models with multiple input and output variables are hard to visualize, and communication about statistical significance and scientific meaning is far from obvious. Here we are studying the transition from single response displays in which the effects of multiple X variables are shown for a singe Y variable towards two classes of dual response graphs: skeletons and flying carpets and then explore how uncertainty of the model can be integrated.
Keywords
Response surfaces, multivariate analysis.
Motivating Example: Polyurethane Foams
Let us start with a practical example. Polyurethane foams used to make mattresses are the result of a simple chemical reaction. In this chemical reaction, a generalized alcohol called a polyol, reacts with isocyanate to form an elastic polymer. At the same time, water also reacts with isocyanate and forms urea and CO2. The urea disperses in the polymer and hardens it, whereas the CO2 forms bubbles which at some time burst into each other to form a breathable foam. Parameters which define the characteristics of the product include hardness, density, tensile strength, and elongation at break. The first two parameters are related to the general hardness and price class of the foam, the second pair to its elastic properties.
Although, the chemistry is quite simple, there are nevertheless a considerable number of variables which determine the foam characteristics. There is the quantity of isocyanate. It is commonly chosen in slight excess to ensure full reaction. Excess isocyanate then dissolves into the urea domains. Furthermore, the amount of water with respect to polyol at equivalent excess isocyanate will create more gas which makes more and larger bubbles and therefore lower density foam. At the same time, the remaining polymer will be harder since it contains more urea. At the same time, less dense foams have less material to hold up the foam and are in general softer.
Further factors determine the characteristics of the product. Additional solids can be added to harden the foam, auxiliary gas generating materials can further reduce density, flame retardants may be needed to pass safety regulation, and air pressure and humidity affect the outcome. This means that the number of input variables and responses and the complexity of the relationship is sufficiently high to make analyzing the relationship quite tricky.
The following graph is an attempt to show how the three most important variables affect the outcome:
Figure 1. Single response graph for IFD hardness of the models presented by R. Schiffauer [1].
This is a single response graph with multiple input variables. Note that the relationships and their relative sizes can be seen for each variable, and one can also compare them. However, no clear summary picture appears. It is also difficult to imagine how to integrate more input variables and how to show interaction effects. Finally, since we wish to understand how the inputs affect multiple responses, several of these graphs have to be studied simultaneously.
Many of us can recall hours of explaining such sets of graphs to the scientists with whom we, statisticians, are collaborating and for whom we have constructed these models.
Skeletons
A first alternative is the skeleton plot for two responses as shown in the example below (Figure 2). Here, one first seeks a hierarchy among the X variables. As a backbone, one selects the variable which has the strongest joint effect on both responses. In the example, this is the water content. Then the effects of other variables are grafted onto the backbone. Variables which show little or no interaction with the backbone variable are grafted once, variables which interact with the backbone variable are grafted twice. Higher order interactions can be added as ‘bones’ grafted at a second level (this is not shown here).
As a result, we obtain a display of a very complex situation in a way which remains interpretable to scientists. In the example, the backbone is perfectly logical: As the water level increases, the foam becomes less dense (more gas) and softer (less substance). Yet, more water also means harder polymer. Higher isocyanate excess (index) or additional solids, increase hardness with little or no effect on density and their effects are a bit different at high density foams made with little water (urea) than at low density foams with a high urea content. Auxiliary blowing agents (here MeCl) and air pressure act in logical and opposite ways … We see, main relationships, although complex can be readily explained and in a way which is much easier and clearer than via a pair of single response graphs.
Figure 2. Skeleton graph of IFD hardness and density based on the models published by R. Schiffauer [1].
The following pair of graphs show a view of two skeleton plots which allow to explore the four responses simultaneously. This display shows at the same time the strength of the method and identifies one difficulty: The backbone of one skeleton graph may not be ideal for another, made for different pair of responses. Developing methods for choosing this variable automatically still need to be designed.
Figure 3. A pair of skeleton plots for the same input variables.
From Skeletons to Flying Carpets
Skeletons help in picturing input output relationships, their sizes, and their interactions. They do not display range of properties which can be attained (under the condition that the model holds). A skeleton lacks flesh. Fleshing out the skeletons means that we have to increase the dimension of the bones to at least 2 and this gets us to flying carpets. A challenge for this display is to identify an anchor point in a visually non-intrusive way.
Figure 4a and b. Fleshing out the backbone representing the water effect by the effect of isocyanate index.
And when there are three input variables, how should we proceed? There are two possibilities: We could go from a two dimensional object (manifold) to a three dimensional one, or we could repeat two dimensional objects. That is, we could go to displays of flying sausages or to multiple flying carpets. The first approach is based on an optical illusion: representing a three dimensional object by showing a visually annotated two dimensional shape. This is very hard to do and also hard to view. The second approach leads to easier displays at the levels of construction and viewing.
Figure 5. Arrangement of Flying Carpets.
And this is about where it ends. Here we show two responses and four input variables to picture the property range in density and hardness which can be covered by the selected formulation range. Skeleton plots can accommodate a few more variables than arrangements of manifolds (flying carpets). In the example, we have six input variables and two responses. These two types of displays are in the following sense optimal: They greatly improve over single response displays by showing more variables and more relationships in a way which is easier to understand. On the other hand, it is not possible to show three responses in a single display since this requires using the illusion of depth. For the same reason, the number of dimensions which can be used in the display object cannot exceed two.
Going beyond two responses requires showing arrangements of two dimensional projections or animation of the graphs.
Ridge Gymnastics
Up to now, we have introduced and discussed skeleton graphs in the case of a known model. In practice, models have to be constructed from data and their parameters are subject to uncertainty. How can one integrate uncertainty with respect to the model and the data?
For this purpose, we shall revisit a complex example reported box Box and Liu [2]. It concerns data collected in the optimization stage in the process of designing paper helicopters which fly when dropped from a bench and whose flight variability is low. There are two responses, flight time in centi-seconds denoted by Y and a measure of variability, 100*log10(stdev(Y)), denoted by LS. There are four input variables, wing area (A), wing length/width ratio (Q), body length (L), and body width (W). The experimental design was a blocked central composite in these four factors.
The following set of dual response display (a mix of flying carpets and skeletons) shows a way of displaying raw data and main patterns. The top left graph shows slices made for the two variables which have the largest overall linear effects, body length (L) and wing length/width ratio (Q). We see a tendency for helicopters with higher wing length/width ratio to fly longer at the expense of variability. For the body length, shorter seems better (note that ‘long’ or ‘short’ are with respect to the chosen experimental ranges. When we blend the linear fits with fits of a full model (including interactions and quadratic terms), we see that the slices separate and become quite irregular when only the full model is shown. The full model over-fits and a reasonable fit is probably somewhere in the middle.
Figure 6. Raw data and models. Top left: linear effects only, slices in wing and body length. Top right: mix of 0.8parts linear and 0.2 parts full model. Bottom left: even mix of linear and full model, bottom right: full model.
Bibliographie
[1] Reinhart Schiffauer (1994), Mathematical Property Prediction Models for Flexible Polyurethane Foams, Proceedings of the 35th Annual Polyurethane Technical/Marketing Conference, 225-238.
[2] G. E. P. Box and P. Liu. Statistics as a Catalyst to Learning by Scientific Method Part I – An Example. Journal of Quality Technology, 31(1):1-15, 1999.