Outlier Screening in Test of Automotive Semiconductors: Use of JMP® Pro 12 Multivariate Analysis Platforms and Explore Outliers Utility
Corinne Bergès, PhD, Six Sigma Black Belt engineer for Analog and Sensors Quality, nxp
1. Introduction
In the semiconductor manufacturing for automotive, the components are subjected to hundreds of parametric tests, at every manufacturing step, from the wafer probe step to the assembly one.
By these tests, we want to screen the likely-to-fail parts, and these likely-to-fail parts show test results far from the normal process variability limits: they are called outliers.
To screen the outliers, the typical tool is study of each test result distribution individually: this type of analysis is called univariate analysis as the opposite of the multivariate analysis where all the tests are studied simultaneously and outliers detected on all the tests, in multivariate.
Here, I present shortly the univariate analysis but above all the multivariate analysis that we tested on a real case study. I present some results.
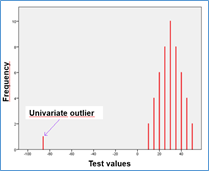
The figure 1. the distribution for a parametric test: we want to detect the part that shows test results far from the normal process variability limits: it is called an outlier, and a univariate outlier in the case of the distribution of only one test.
Figure 1: distribution for a parametric test
There will be four chapters in this presentation.
A first chapter will describe several techniques that are possible to be run with jmp. Last year, they have been tested for an automotive valve driver, and how they are launched and run with jmp will be presented.
That will be the opportunity to discuss about space size in a second chapter, and efficiency and yield loss in a third chapter.
Finally a fourth chapter will present a specific platform in jmp to screen the outliers.
2. Some multivariate technics with jmp
There are two types of multivariate analysis:
-the analysis that don’t need a learning step;
-and the analysis that need a learning step on first customer returns.
- Methods without learning step
The methods without learning step are based on a threshold and that threshold is directly linked to the yield loss. So, the challenge is to set a threshold capable to detect outliers and returns with a low yield loss.
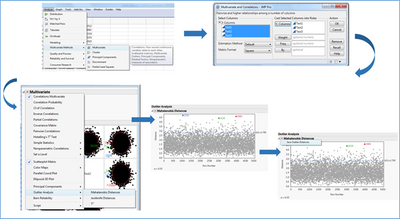
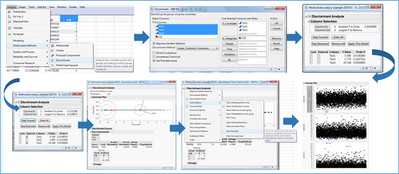
The first multivariate analysis without learning presented here is an estimation of the Mahalanobis distance. The Mahalanobis distance is a spatial distance as the Euclidian distance is in a 2-dimension space. It is based on variance-covariance estimation on a matrix containing all the test results.
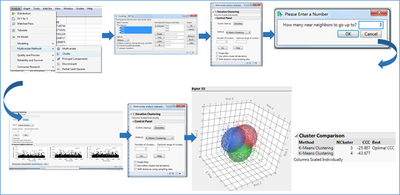
The second method is the k-means clustering method. It consists in building of k groups or clusters, one part being assigned to the nearest cluster.
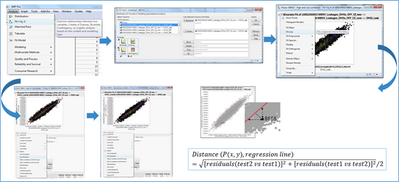
The third method used is deviation estimation from a linear regression: in that case, tests are studied two by two. It is a bivariate method used when the tests are highly correlated.
- Methods needing a learning step
In the second type, the learning step aims to build the model that will be used to detect outliers from the following manufactured parts. The risk is to build a model that sticks too much to the first sample that contained the first returns and that may be not able to detect outliers and returns from another sample: it’s the overfitting risk.
In the discriminant analysis, we search a test result combination that allows to predict if a part is failing or not: it is about again a Mahalanobis distance. For that test combination, the distance is maximal between the two groups.
In the Partial Least Square, we search to select tests where the variance that is to say the data brought by them, is maximal but also where correlation between parts and response ‘failed or not’ is maximal.
- Yield loss
We will speak later about yield loss: all the outliers are not going to fail and decision for rejecting of more outliers fits with decrease risk to have returns but directly fits also with a higher yield loss. A method will succeed in detection if the yield loss is low: it is a success criteria.
- How to do with jmp ? Case study for an automotive valve driver
Now, we present some results obtained with several methods from the two types, with or without learning step. The case study is an automotive driver part. On one return, the typical univariate analysis failed to detect abnormality on the failed part. For the analysis, we used a file of 745 tests and 13 000 parts, including the return.
So, the mutivariate analysis have been run on a space size of 13 000 parts and 745 tests.
The question is: what is the best multivariate method to detect the customer return in multivariate ?
See the scripts saved in the files: ‘Multivariate analysis.jmp’, ‘Bivariate and PCA.jmp’ and ‘Partial Least Square.jmp’.
Figure 2: Mahalanobis distance estimation
Figure 3: K-means clustering method
Figure 4: Deviation estimation from a linear regression
Figure 5: Discriminant analysis
Figure 6: Partial Least Square (PLS)
Finally, for our case study, best multivariate method without learning is the Mahalanobis distance, that succeeds to detect the return with a yield loss of 0.36%. We will see later how to reduce this yield loss that is too important.
For our same case study, methods with learning failed; one reason seems to be that the group of failing parts is constituted only by one return.
So, Mahalanobis distance without learning stays the best multivariate method in that case. But, again, yield loss is far too high.
3. Space size
Let’s remind that space size is defined by the number of tests and the number of tested parts. Size reduction fits with selecting of some tests which the multivariate analysis will be performed on.
An analysis on a high space size takes computing resources, time and therefore cost, which motivate to reduce space size. But there are other reasons to reduce space size: we obtain better results on reduced space when the useful data is concentrated rather than diluted on a lot of test results. The multivariate analysis work better also on correlated tests.
With test reduction, we reduce also the overfitting risk.
It is possible to reduce space size, reducing the number of parts, too: it may be the opportunity to reduce noise selecting the parts from homogeneous data: for example, the results will be better performing an analysis on a wafer lot, at the probe step, rather than performing it at the assembly test, on several wafer lots, with more parts.
There are 3 means to reduce space size:
-the first one is a statistical analysis, like a Principal Component Analysis (PCA);
-the second one may be functionality criteria when we want to focuse on some functional blocks, for example;
-the third one is linked to noise reduction as I already told earlier, focusing on a wafer lot.
We performed a typical PCA on the automotive valve driver of our case study: unfortunately, after a space size reduction, yield loss was higher to detect the same return. That seems coherent with the fact that a PCA is going to search for majority data.
Figure 7: Principal Component Analysis
4. Efficiency and yield loss
We are going to speak again yield loss: efficiency of a method is measured by yield loss in relation with rejection level. A real mean to increase efficiency is noise reduction. Noise may be linked to the test conditions, for example when the gage has been poorly studied.
For the case study, we wanted to vizualize noise due the 4 sites on which the parts were tested, with some statistical analysis (‘noise analysis.jmp’).
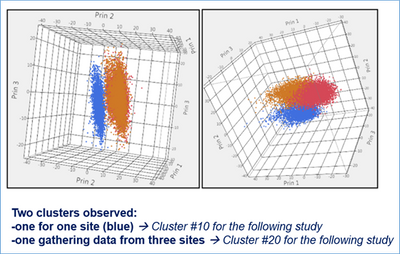
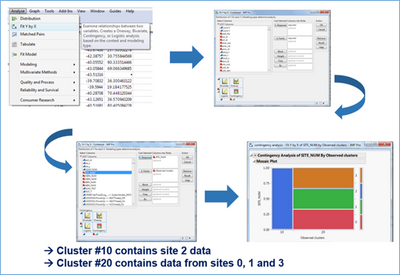
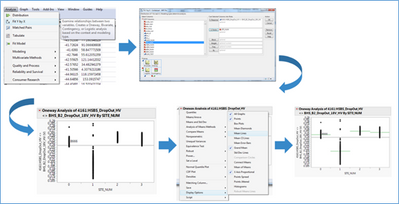
The first one is a new k-means clustering method led on the test results: we succeeded to clearly see two clusters. One of them gathered data from only one test site. And the other one, the 3 other sites. This result was confirmed by a contingency analysis. It is always possible to lead a more typical ANOVA analysis. In that example on one test, we see clearly that a mean for one site is different from the three other ones.
Figure 8: K-means clustering method to visualize tester variability
Figure 9: Contingency analysis
Figure 10: ANOVA
Finally, the best opportunity to reduce noise is of course to lead a gage study and to take corrective actions against the noise sources revealed by the gage study. For this case study, where the noise is found after part tests, a possibility could be to shift and to align all the means for each site. That decreases yield loss.
5. ‘Explore Outliers’ jmp platform
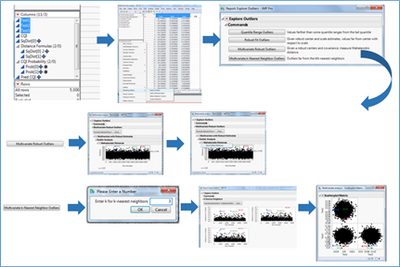
Another quick possibility to screen outliers and remove them from a data file is the new ‘Explore Outliers’ platform. The last two options on that platform fit with multivariate analysis of Mahalanobis distance estimation and k-means clustering method.
Figure 11. ‘Explore Outliers’ utility
6. Conclusion
When we decide to run a multivariate analysis, the first step will be a gage study before part test or noise reduction after part test. Univariate analysis will take advantage of that as much as the multivariate ones.
Second step is to run the multivariate analysis. Mahalanobis distance is the most used spatial distance. Implementation challenges or difficulties are different if the method is either with or without learning step.
The last step fits with method validation: whatever the new method chosen, it is very important to validate its implementation on several manufacturing months. A good method has to detect efficiently outliers, likely-to-fail parts, with the lowest possible yield loss.
Corinne Bergès, PhD, Six Sigma Black Belt engineer for Analog and Sensors Quality, nxp
1. Introduction
In the semiconductor manufacturing for automotive, the components are subjected to hundreds of parametric tests, at every manufacturing step, from the wafer probe step to the assembly one.
By these tests, we want to screen the likely-to-fail parts, and these likely-to-fail parts show test results far from the normal process variability limits: they are called outliers.
To screen the outliers, the typical tool is study of each test result distribution individually: this type of analysis is called univariate analysis as the opposite of the multivariate analysis where all the tests are studied simultaneously and outliers detected on all the tests, in multivariate.
Here, I present shortly the univariate analysis but above all the multivariate analysis that we tested on a real case study. I present some results.
The figure 1. the distribution for a parametric test: we want to detect the part that shows test results far from the normal process variability limits: it is called an outlier, and a univariate outlier in the case of the distribution of only one test.
Figure 1: distribution for a parametric test
There will be four chapters in this presentation.
A first chapter will describe several techniques that are possible to be run with jmp. Last year, they have been tested for an automotive valve driver, and how they are launched and run with jmp will be presented.
That will be the opportunity to discuss about space size in a second chapter, and efficiency and yield loss in a third chapter.
Finally a fourth chapter will present a specific platform in jmp to screen the outliers.
2. Some multivariate technics with jmp
There are two types of multivariate analysis:
-the analysis that don’t need a learning step;
-and the analysis that need a learning step on first customer returns.
- Methods without learning step
The methods without learning step are based on a threshold and that threshold is directly linked to the yield loss. So, the challenge is to set a threshold capable to detect outliers and returns with a low yield loss.
The first multivariate analysis without learning presented here is an estimation of the Mahalanobis distance. The Mahalanobis distance is a spatial distance as the Euclidian distance is in a 2-dimension space. It is based on variance-covariance estimation on a matrix containing all the test results.
The second method is the k-means clustering method. It consists in building of k groups or clusters, one part being assigned to the nearest cluster.
The third method used is deviation estimation from a linear regression: in that case, tests are studied two by two. It is a bivariate method used when the tests are highly correlated.
- Methods needing a learning step
In the second type, the learning step aims to build the model that will be used to detect outliers from the following manufactured parts. The risk is to build a model that sticks too much to the first sample that contained the first returns and that may be not able to detect outliers and returns from another sample: it’s the overfitting risk.
In the discriminant analysis, we search a test result combination that allows to predict if a part is failing or not: it is about again a Mahalanobis distance. For that test combination, the distance is maximal between the two groups.
In the Partial Least Square, we search to select tests where the variance that is to say the data brought by them, is maximal but also where correlation between parts and response ‘failed or not’ is maximal.
- Yield loss
We will speak later about yield loss: all the outliers are not going to fail and decision for rejecting of more outliers fits with decrease risk to have returns but directly fits also with a higher yield loss. A method will succeed in detection if the yield loss is low: it is a success criteria.
- How to do with jmp ? Case study for an automotive valve driver
Now, we present some results obtained with several methods from the two types, with or without learning step. The case study is an automotive driver part. On one return, the typical univariate analysis failed to detect abnormality on the failed part. For the analysis, we used a file of 745 tests and 13 000 parts, including the return.
So, the mutivariate analysis have been run on a space size of 13 000 parts and 745 tests.
The question is: what is the best multivariate method to detect the customer return in multivariate ?
See the scripts saved in the files: ‘Multivariate analysis.jmp’, ‘Bivariate and PCA.jmp’ and ‘Partial Least Square.jmp’.
Figure 2: Mahalanobis distance estimation
Figure 3: K-means clustering method
Figure 4: Deviation estimation from a linear regression
Figure 5: Discriminant analysis
Figure 6: Partial Least Square (PLS)
Finally, for our case study, best multivariate method without learning is the Mahalanobis distance, that succeeds to detect the return with a yield loss of 0.36%. We will see later how to reduce this yield loss that is too important.
For our same case study, methods with learning failed; one reason seems to be that the group of failing parts is constituted only by one return.
So, Mahalanobis distance without learning stays the best multivariate method in that case. But, again, yield loss is far too high.
3. Space size
Let’s remind that space size is defined by the number of tests and the number of tested parts. Size reduction fits with selecting of some tests which the multivariate analysis will be performed on.
An analysis on a high space size takes computing resources, time and therefore cost, which motivate to reduce space size. But there are other reasons to reduce space size: we obtain better results on reduced space when the useful data is concentrated rather than diluted on a lot of test results. The multivariate analysis work better also on correlated tests.
With test reduction, we reduce also the overfitting risk.
It is possible to reduce space size, reducing the number of parts, too: it may be the opportunity to reduce noise selecting the parts from homogeneous data: for example, the results will be better performing an analysis on a wafer lot, at the probe step, rather than performing it at the assembly test, on several wafer lots, with more parts.
There are 3 means to reduce space size:
-the first one is a statistical analysis, like a Principal Component Analysis (PCA);
-the second one may be functionality criteria when we want to focuse on some functional blocks, for example;
-the third one is linked to noise reduction as I already told earlier, focusing on a wafer lot.
We performed a typical PCA on the automotive valve driver of our case study: unfortunately, after a space size reduction, yield loss was higher to detect the same return. That seems coherent with the fact that a PCA is going to search for majority data.
Figure 7: Principal Component Analysis
4. Efficiency and yield loss
We are going to speak again yield loss: efficiency of a method is measured by yield loss in relation with rejection level. A real mean to increase efficiency is noise reduction. Noise may be linked to the test conditions, for example when the gage has been poorly studied.
For the case study, we wanted to vizualize noise due the 4 sites on which the parts were tested, with some statistical analysis (‘noise analysis.jmp’).
The first one is a new k-means clustering method led on the test results: we succeeded to clearly see two clusters. One of them gathered data from only one test site. And the other one, the 3 other sites. This result was confirmed by a contingency analysis. It is always possible to lead a more typical ANOVA analysis. In that example on one test, we see clearly that a mean for one site is different from the three other ones.
Figure 8: K-means clustering method to visualize tester variability
Figure 9: Contingency analysis
Figure 10: ANOVA
Finally, the best opportunity to reduce noise is of course to lead a gage study and to take corrective actions against the noise sources revealed by the gage study. For this case study, where the noise is found after part tests, a possibility could be to shift and to align all the means for each site. That decreases yield loss.
5. ‘Explore Outliers’ jmp platform
Another quick possibility to screen outliers and remove them from a data file is the new ‘Explore Outliers’ platform. The last two options on that platform fit with multivariate analysis of Mahalanobis distance estimation and k-means clustering method.
Figure 11. ‘Explore Outliers’ utility
6. Conclusion
When we decide to run a multivariate analysis, the first step will be a gage study before part test or noise reduction after part test. Univariate analysis will take advantage of that as much as the multivariate ones.
Second step is to run the multivariate analysis. Mahalanobis distance is the most used spatial distance. Implementation challenges or difficulties are different if the method is either with or without learning step.
The last step fits with method validation: whatever the new method chosen, it is very important to validate its implementation on several manufacturing months. A good method has to detect efficiently outliers, likely-to-fail parts, with the lowest possible yield loss.