Level: Intermediate
Laura Castro-Schilo, JMP Senior Associate Research Statistician Developer, SAS
Multivariate data analysis has become an essential skill as the amount of data has skyrocketed and companies become more data-driven in their decision making. In this session, we showcase JMP and its unique visual and interactive approach to multivariate data analysis using a variety of approaches that rely on continuous, categorical and multiple-source data. We will begin with a foundational discussion of the essence of multivariate analysis: the idea that information contained in large numbers of variables can often be efficiently represented with a smaller number of variables. We then give an overview of general tools for analyzing multivariate data in JMP. We will use data from sensory analysis and consumer research to motivate and demonstrate classic unsupervised multivariate methods such as principal components analysis (PCA), multiple correspondence analysis (MCA) and a new technique in JMP 14, multiple factor analysis (MFA). Throughout, we will give clear guidelines as to when each analytical technique is appropriate and highlight the most important and useful software options.
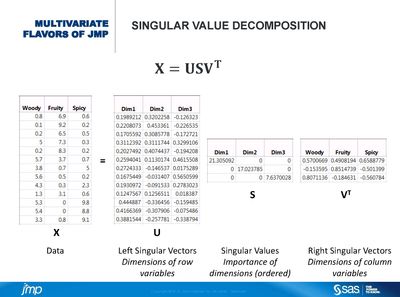
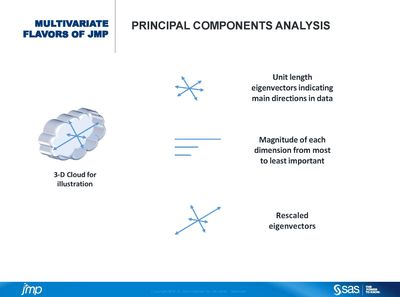
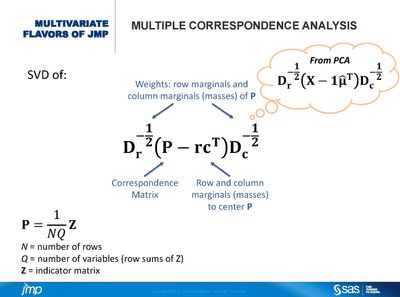
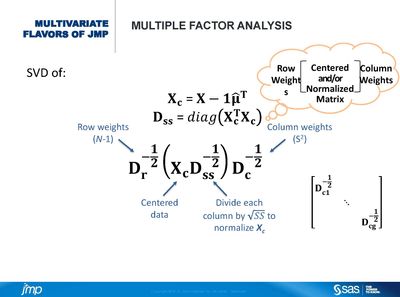
JMP has a variety of flavors of multivariate techniques. One thing they all have in common is they aim to identify the basic structure of the data matrix they are applied to. Some techniques rely on this basic structure to reduce the dimensionality of the data at hand and facilitate their understanding. A tool that enables us to find the basic structure of a matrix is the singular value decomposition (SVD). The SVD produces vectors, which represent the dimensions of rows and columns of the matrix. It also produces singular values, which represent the importance of each of the dimensions. The multivariate techniques described in this session are based on using the SVD on transformed matrices and applying weights to rows, columns, or both. We will describe each of the techniques (PCA, MCA, and MFA) by emphasizing their similarities. Our goal is to improve the use and understanding of these techniques by using a common framework to describe them. Paired with demos and examples, this session prepares the audience to explore multivariate continuous, categorical, and multiple-source data.