- JMP User Community
- :
- Discussions
- :
- Can you use the Equivalence of means sample size calculator for attribute data?
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Can you use the Equivalence of means sample size calculator for attribute data?
Hi, Maybe i'm using the wrong type of test..but I would like to generate a sample size to compare two parts. The test is an attribute test and I just want to verify the new part doesn't increase the failures by more than 10%. This seemed like a non inferiority test when I first thought about it but playing around with the calculator, it seems like it's more of a test for variable data. Am I just thinking about the wrong test or is there a way to adapt the calculator for attribute data? Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Can you use the Equivalence of means sample size calculator for attribute data?
Hi @SerialDeviation : It might help to put the problem in the framework of hypotheses testing.
Suppose p1 is the failure rate for the old part, and p2 is the failure rate for the new part.
Do you want to "prove" p2-p1<0.10? (i.e., and absolute difference of no more than 10%):
If so, your null and alternative hypotheses are:
H0: p2-p1=0.1.
Ha: p2-p1<0.1.
Then this is indeed an NI study, you have to ask yourself some questions:
(1). Are the failure rates independent? i.e., does part 1 failing influence whether part 2 fails or not (or visa-versa)?
(2). What information do you have about p1 and p2?
(3). What is your desired Type 1 error rate?
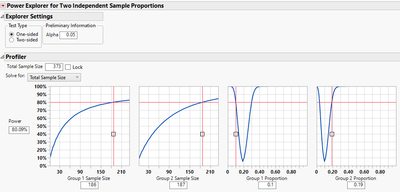
Let's suppose the answer to (1 ) is yes (they are independent), and you (2) expect the true proportions to be p1 = 0.1 and p2 = 0.19, and (3) Type 1 error rate (alpha) = 0.05.. Then you can use the "Power Explorer for Two Independent Sample Proportions" as shown below if you want 80% power:
If, however, your alternative (the thing you want to "prove") is:
Ha: p2/p1<1.1 then that is a different animal (that is a relative difference of 10%).
- © 2024 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- About JMP
- JMP Software
- JMP User Community
- Contact