- JMP User Community
- :
- Discussions
- :
- How can I do a chi-square test when 20% of the cells that have an expected count...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How can I do a chi-square test when 20% of the cells that have an expected count less than 5?
I've got these warning messages (see below) after doing some analysis with some variables. So to fix this problem, I read in a stats book that I need to follow some steps that it stated in order to correct the problem such as "If the smallest expected cell frequency is less than five, the analyst should recode a row or column variable, combining rows or columns until an adequate expected cell frequency is achieved."
However, I don't really understand this or how to do it in JMP. Can someone explain how I might change modify things so that I won't get his warning message either through the instructions from the book I've just mentioned or from a better way? I've also heard that I one can alternatively use the fisher's test?
Thanks!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I correct the cells that have an expected count less than 5?
The Chi square test used in the Contingency platform requires at least 80% of the cells to have an expected count greater than 5 or else the sum of the cell Chi squares will not have a Chi square distribution and so your test (p-value) will not be valid.
The usual, simple solution in such cases is to combine levels. For example, in your case you might replace the five levels with just three (Disagree, Neutral, Agree) and see if your assumption is valid. This way does not exclude any data from the analysis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I correct the cells that have an expected count less than 5?
I made a quick scan of your results( which means my statistical viewpoint may be less than accurate), it appears that few respondants have answered "Disagree" or "Strongly Disagree". So you may want to do one of 2 things. Either eliminate those respondants, or recode their answers.
To eliminate those responses, you can open up a local data filter by going to the red triangle at the top of the display, and selecting Local Data Filter. There you will be able to select only the data you want. You can also go to the data table, Select all rows that match either of the choices, and then right click on the row state column for one of the selected rows, and select "Hide and Exclude". When you rerun the analysis those rows will be left out of the analysis.
If you want to recode, then go to the column in question, "Recycling can.........", select that column, and then in the Columns Panel at the left of the data table click on the red triangle and select Recode. The window that pops up will let you combine the Disagree and Strongly Disagree or maybe to take both of these choices and move them into Neutral
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I correct the cells that have an expected count less than 5?
But if I eliminate those responses, won't that also eliminate their data from my analysis which would alter the results since I'm excluding some responses? I'm not really sure how eliminating respondants fixes the problem; which respondents should I eliminate? Could you explain how doing either these two might fix my problem as I'm having a hard time understanding the concept. Because from what I see, if I combine columns, then how about the data within the columns that had a few responses? Isn't that information useful even if just one person selected that option such as the "I don't know" option? Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I correct the cells that have an expected count less than 5?
Your concerns are valid. And what I illustrated is a method to allow you to collapse or eliminate data so that you can meet the requirements of the statistical test. But as you indicate, that method comes with a cost.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I correct the cells that have an expected count less than 5?
So is there any way to fix this issue without altering the data significantly? Or will the methods that you mentioned not significantly affect the results?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I correct the cells that have an expected count less than 5?
The data are, what the data are. The statistics are based upon the relationships with between the different cells. You may be able to overcome the issue by increasing the number of data points, but that would require getting more subjects. Any concatenations, or eliminations that you choose to do, need to be evaluated from the real world. Many times, the very small cell counts are meaningless because of the low number of responses. In those cases, you really can not draw any opinion on those results anyway. So even if you left them in, I would not want to make any statement on those cells anyway. Taking them out, therefore, may allow you to show stronger relationships with the remaining data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I correct the cells that have an expected count less than 5?
The Chi square test used in the Contingency platform requires at least 80% of the cells to have an expected count greater than 5 or else the sum of the cell Chi squares will not have a Chi square distribution and so your test (p-value) will not be valid.
The usual, simple solution in such cases is to combine levels. For example, in your case you might replace the five levels with just three (Disagree, Neutral, Agree) and see if your assumption is valid. This way does not exclude any data from the analysis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I correct the cells that have an expected count less than 5?
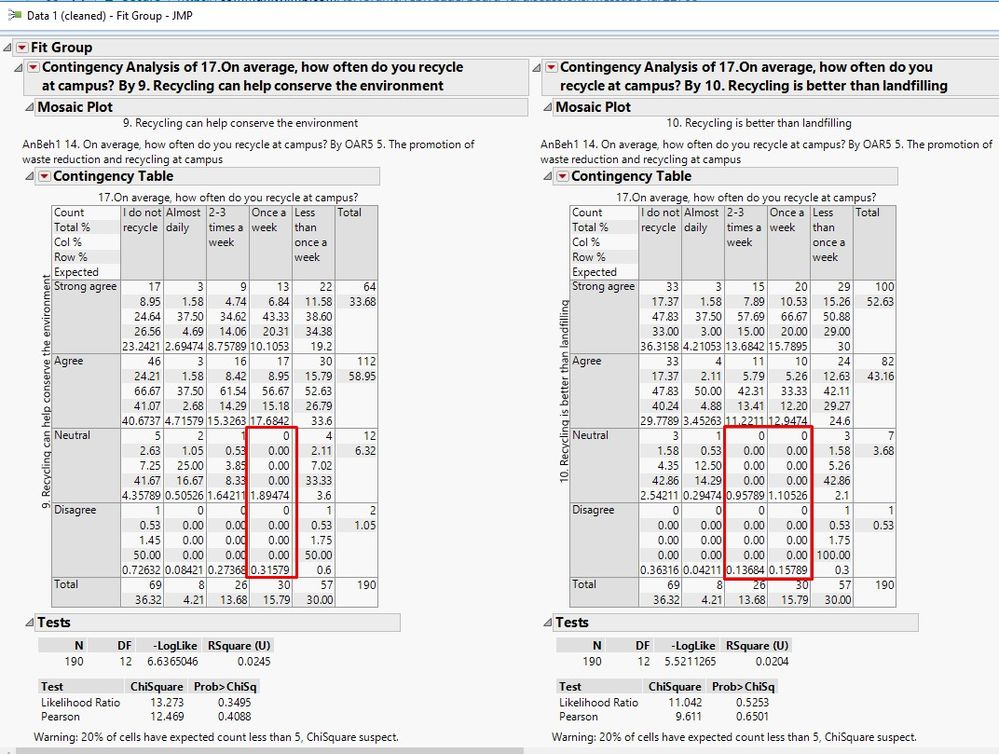
Thanks you both for your answers, I found them to be very helpful. But I found another problem in other parts of my data. Your solution to combine levels and to have just 3 levels does work in some circumstances. But in the below results, I don't think I can do this as you can see there are just too many cells that have zero expected values in multiple levels, making it hard to combine them. I think then, the Fisher's exact test is the last resort that I have to fix this problem. But I would like to ask how can I do the Fisher's test in JMP when my variables have multiple categories resulting in tables that have numerous rows/columns (e.g 4x5, 5x5) while Fisher's exact test requries a 2x2 table?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I correct the cells that have an expected count less than 5?
First of all, a clarification: the validity is not based on zero counts, but cells with expected counts less than five.
JMP provides the exact test only for 2x2 contingency tables. JMP Pro or SAS/STAT provides the exact test for larger tables.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I correct the cells that have an expected count less than 5?
Yes, I am aware that the validity is based on cells with expected count less than 5, I just highlighted those cells to show why I wouldn't be able to combine the levels since there were cells with expected count less than 5 on both the neutral and the disagree levels.
Well it is unfortunate that I would need to get those software in order to do this test. So is there any other solution for my problem?
- © 2024 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- About JMP
- JMP Software
- JMP User Community
- Contact