JMP 18の新機能 Part 2：データ探索に便利な機能と予測プロファイルのアップデート

[#1]

前回のブログ(Part 1)　では、JMP 18で強化された「Pyhtonインテグレーション」の機能を用いて、scikit-learnのサンプルデータ「カリフォルニアの住宅価格」をJMPのデータテーブルとして読み込む方法をご紹介しました。

今回のブログ（Part 2）では、読み込んだデータを用いて、住宅価格を築年数、部屋数、緯度、経度などから予測する回帰モデルを作成し、予測プロファイルを使ってモデルを視覚化します。その際、JMP 18ではプロファイルで予測区間を表示できるようになりましたので、この機能も活用してみます。

ただし、データを観察せずいきなりモデルを作成することは危険ですので、グラフ化や要約によってデータを探索してみます。JMP 18では、データを探索するのに便利な機能も追加されています。

ヘッダ統計量、列スイッチャーによるデータ探索

JMPでデータを探索する際、JMP 18の新機能である「ヘッダ統計量」、「列マネージャー」の利用をおすすめします。

ヘッダ統計量

データテーブルにあるΣのアイコンをクリックすると、各列の要約統計量がデータテーブルに表示されます。さらに既存のJMPの機能ではありますが、ヒストグラムのアイコンをクリックしヘッダグラフも表示でき、これにより大まかなデータの視覚化と要約が可能になります。

列マネージャー

列パネルにアイコン（上記、緑の丸で示される部分）をクリックすると、以下のような列マネージャーが起動します。このツールを使用して列プロパティの変更や要約統計量、分布などを表示でき、特に変数が多いデータの要約に非常に便利です。

要約統計量や分布をみると、いくつかの変数でデータが右側に裾を引いて、異常値ともいえる大きな値があることがわかります。たとえば、AveRooms(そのブロックにおける平均部屋数)の最大値は141.9、AveBedrms（そのブロックにおける平均寝室数）の最大値34です。141部屋あり、寝室が34部屋がある家に住むなんで私のような庶民では全く想像できません。。

しかし、これらの異常値は後に作成するモデルに影響を及ぼす可能性があるため、目的変数および説明変数を使用して多変量の距離（マハラノビス距離）を算出し、値が大きいデータをモデル作成から除外することにしました。

このプロセスで17個のデータを除外しました。これらのデータをデータテーブルから除外すると、ヘッダグラフやヘッダ統計量はそれに応じて再計算されます。

「予測プロファイル」で予測区間を表示

[モデルのあてはめ]を用いて、カリフォルニアの住宅価格（MedHouseVal）を、それ以外の変数（MedIncやHouse Ageなど）の主効果で説明するモデル（以下、主効果モデル）を作成したときのレポートは以下の通りです。

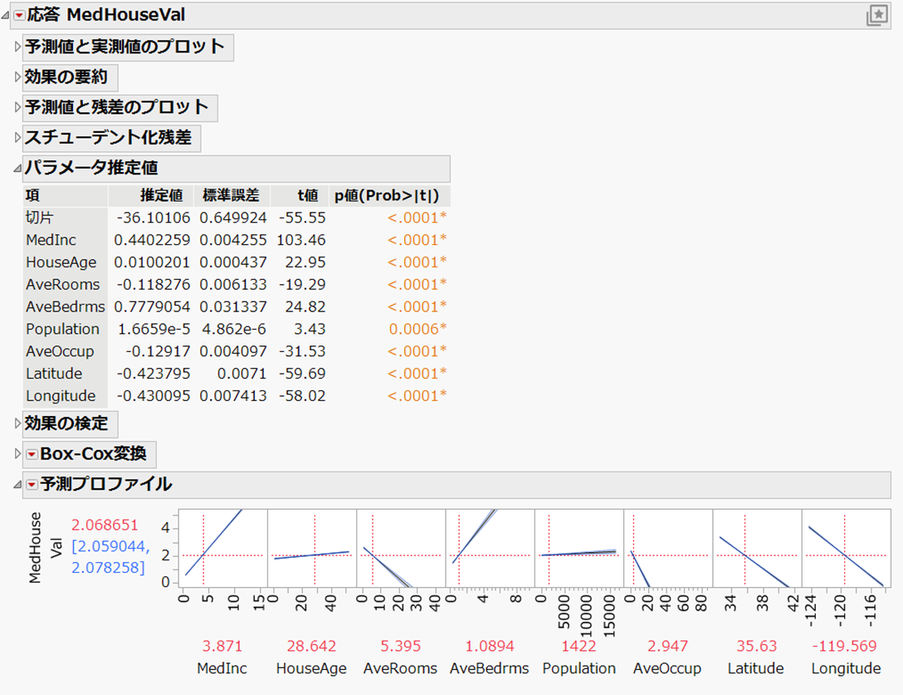
レポート「パラメータ推定値」の推定値が回帰モデルにおける偏回帰係数となりますが、このモデル式を可視化したものが「予測プロファイル」です。平均部屋数（AveRooms）が多いほど価格が下がるという関係が示されていますが、これは直感とは異なるかもしれません。ただし、ここでは得られた予測式に基づきます。

また、異なるブロックでの住宅価格を予測する際、予測値の取りうる値の範囲を考える場合は、予測区間を利用することが望ましいです。JMP 18では、予測プロファイルの左にある赤い三角ボタンから「予測区間」を選択することで、95%予測区間（緑色の直線が信頼限界を示す）を表示できます。

この予測式をもとに、カリフォルニアの別のブロックにおける住宅価格をそのブロックのパラメータ（収入、築年、部屋数など）から予測するといった場合、予測の範囲として予測区間を求めることが望ましいです。

JMP  18では、「予測プロファイル」の左にある赤い三角ボタンから[予測区間] を選択することにより、以下のような95%予測区間（緑色の直線が95%予測区間の信頼限界）を表示できます。

さらにJMP 18では、[グラフ] メニューにある [プロファイル] でも、信頼区間や予測区間を表示することができます。

以下の図のように、[列の保存] > [予測値と区間の計算式]　を選択します。すると、データテーブルに予測式と信頼区間（平均、個別）の列が追加されます。

※信頼区間の列は、"表示しない" 設定になっています。

このプロセスでは、主効果モデルに加えて、主効果と2次の交互作用を含めたモデルも作成し、同様の手順で計算式を保存しています。

"主効果のモデル"と"主効果+2次の交互作用モデル" のプロファイルを比較するために、[グラフ] > [プロファイル]を用いて、先ほど保存した予測式の列を [Y,予測式]の列に指定します。

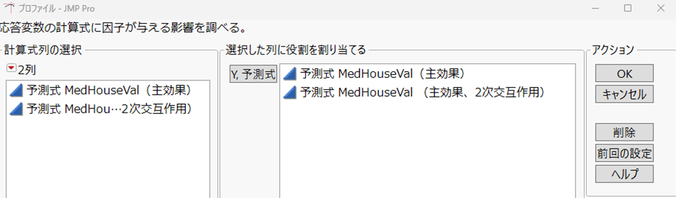
プロファイルのレポートが表示されますので、「予測プロファイル」の左にある赤い三角ボタンから [予測区間] を選択し、[信頼区間]のチェックを外したものが下図です。

上記のプロファイルは、カリフォルニアの経度-122.23, 緯度37.88で、収入が8、築年数が2、部屋数が7・・・というブロックがあったとき、住宅の中央値価格の予測値とその95%予測区間を示しています。

モデル	予測値と95%予測区間
主効果モデル	3.91 [2.53, 5.29]
主効果、2次交互作用モデル	4.14 [2.80, 5,47]

2つのモデルを比較すると、予測値と予測区間に若干の違いがあります。しかし、住宅価格の予測値としては約4と考え、予測の幅は2.5から5.5の範囲で考慮すると良いでしょう。

by  増川 直裕（JMP Japan）

Naohiro Masukawa - JMP User Community