- JMP User Community
- :
- Blogs
- :
- Uncharted
- :
- Bezier Tree using Path()
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
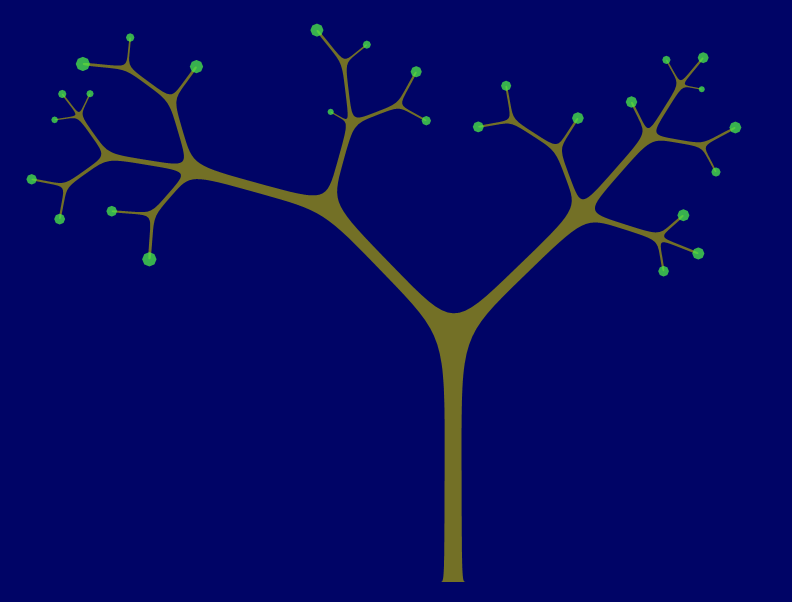
Similar to Recursive Tree Generator , but a bit more organic. This implementation uses Bezier curves to outline the trunk, limbs, and twigs. When the twigs are divided too finely, a clump of leaves is added. The JSL path(...) function is used to draw the Bezier trunk and the leaves, though the leaves are just an octagon. When a path is filled, and it crosses over itself, it does an even-odd count to determine if the fill color is applied. With the twigs this isn't really desirable, but with the leaves it makes a nice effect.

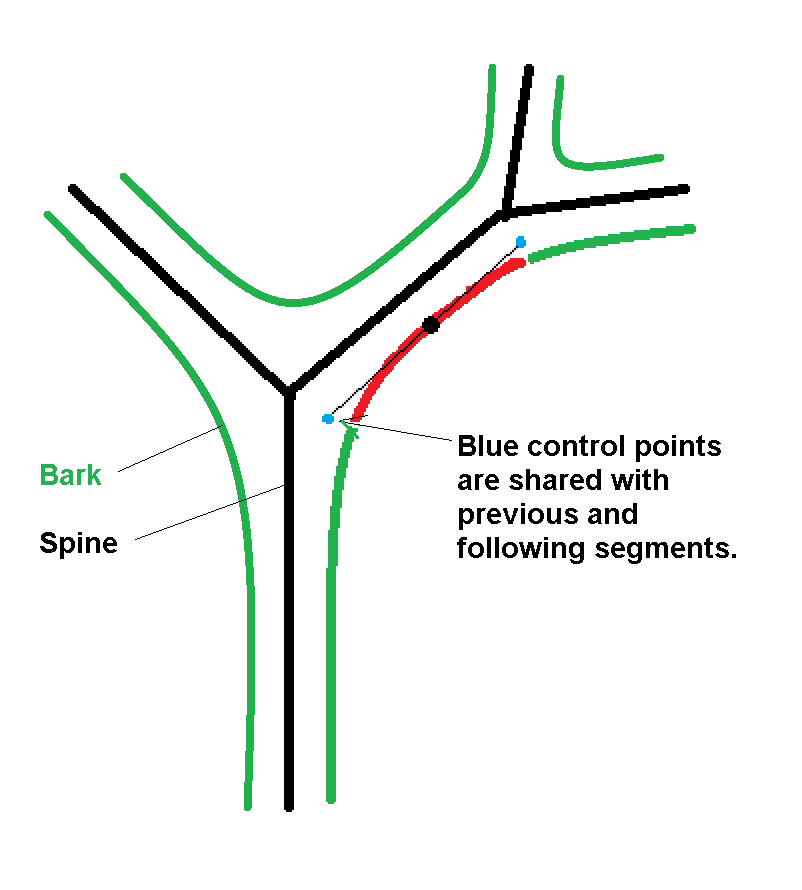
Internally, the algorithm creates a random shaped tree, following the central spine of each trunk/limb/twig and recording the Bezier points for the left side on the way to the leaves and the Bezier points for the right side on the way back to the trunk. The point that is on the center of a segment is a drawn point; the two control points on each side are where the segment meets other segments.
Changing the minimum limb size controls how deep the recursion goes; some of these turned off the leaves for clarity.







// Recursive routine builds a random tree using Bezier curves in path(...) command
TreePath = Function( {x0, y0, size0, angle},// parameters for recursion
{x0L, x0R, y0L, y0R, x1, y1, size1, x1L, x1R, y1L, y1R, nbranches, leftangle, rightangle, ibranch, nbranches, angles, length, biggest, biggestv,
middle, middlev, cx0, cy0, cx1, cy1, cxc, cyc, xcleaf, ycleaf, radleaf, xleaf, yleaf, diameter, leafangle}, // local variables
// x0,y0 is the center of this trunk segment, starting point. angle is the direction, and size0 the radius.
leftangle = angle + Pi() / 2; // find two points at right angles to the direction of growth
rightangle = angle - Pi() / 2; // by adding +/- 90 degrees ... this is all radians, so PI/2
x0L = x0 + size0 * Cos( leftangle ); // size0 is the radius
y0L = y0 + size0 * Sin( leftangle );
x0R = x0 + size0 * Cos( rightangle );
y0R = y0 + size0 * Sin( rightangle );
length = size0 ^ 1 * Abs( Random Normal( 30, 2 ) );// scaling constants...play with these
size1 = .95 * size0;// .95 is a limb shrinkage constant. Not sure this is enough to notice the taper.
x1 = x0 + length * Cos( angle ); // x1,y1 is the other endpoint of this trunk segment
y1 = y0 + length * Sin( angle );
x1L = x1 + size1 * Cos( leftangle ); // and similar right angle calculation
y1L = y1 + size1 * Sin( leftangle ); // to find the bark at the other end
x1R = x1 + size1 * Cos( rightangle );
y1R = y1 + size1 * Sin( rightangle );
// the center of the trunk segment is ON the drawn curve. the endpoints become
// control points that pull the curve toward the joints, partway, leaving smooth bends.
Insert Into( global:pathTrunk, Eval List( {Eval List( {x0L, y0L, 0 /*control*/} )} ) );
Insert Into( global:pathTrunk, Eval List( {Eval List( {(x0L + x1L) / 2, (y0L + y1L) / 2, 3/*bezier*/} )} ) );
Insert Into( global:pathTrunk, Eval List( {Eval List( {x1L, y1L, 0 /*control*/} )} ) );
If( size0 > .5, // the recursion stops when the branch becomes twigs; leaves are added then <grin>
nbranches = Random Integer( 2, 3 ); // experiment with number of branches here
angles = J( nbranches, 1, Abs( Random Normal( 4, 1 ) ) );
// I decided the trees generally looked better if the bigger branch was centered...
biggest = Loc Max( angles );
biggestv = angles[biggest];
middle = Ceiling( N Rows( angles ) / 2 );
middlev = angles[middle];
angles[middle] = biggestv;
angles[biggest] = middlev;
angles = angles / Sum( angles ) * Pi();//normalize, radians
// repurpose leftangle and rightangle, using previous leftangle as a starting point:
// there is a semicircle at the end of this branch, pi() radians (180 deg), going through
// x1L,y1L and x1R,y1R which form a diameter. The first branch leaves from x1L,y1L and
// the rightangle on the semicircle (computed inside the loop.) The angle is half way,
// and the x0y0 is on the chord, halfway. When this routine is recursively called,
// it will recompute the two points on the chord from the angle and size, which is half the chord length.
For( ibranch = 1, ibranch <= nbranches, ibranch += 1,
// working on a branch...figure out its base
rightangle = leftangle - angles[ibranch];
// x1,y1 is the semicircle center. get the chord endpoints at the left and right angles and radius size.
cx0 = x1 + size1 * Cos( leftangle );
cy0 = y1 + size1 * Sin( leftangle );
cx1 = x1 + size1 * Cos( rightangle );
cy1 = y1 + size1 * Sin( rightangle );
// and the midpoint of the chord
cxc = (cx0 + cx1) / 2;
cyc = (cy0 + cy1) / 2;
// and the diameter of the branch (length of chord)
diameter = Sqrt( (cx0 - cx1) ^ 2 + (cy0 - cy1) ^ 2 );
// here it is! do the child branch (which will do its child...)
Recurse( cxc, cyc, diameter / 2, (leftangle + rightangle) / 2 );
// set up for next branch...
leftangle = rightangle;
);
, //else cap this branch and add the leaves
// the cap is a rounded line across the end instead of more branching
Insert Into( global:pathTrunk, Eval List( {Eval List( {x1L, y1L, 0 /*control*/} )} ) );
Insert Into( global:pathTrunk, Eval List( {Eval List( {(x1L + x1R) / 2, (y1L + y1R) / 2, 3/*bezier*/} )} ) );
Insert Into( global:pathTrunk, Eval List( {Eval List( {x1R, y1R, 0 /*control*/} )} ) );
// add leaves to the twigs...circle diameter twig length, centered on twig...
// the single path with all these circles makes an interesting pattern when the circles overlap
// and cancel each other out in an even/odd way. The trunk does that too, and there seems to be no way to prevent it.
xcleaf = (x1L + x1R) / 2; // center a sphere of leaves over the cap segment
ycleaf = (y1L + y1R) / 2;
radleaf = 100 * size1; // constant to play with - radius of leaf ball around cap's size
For( leafangle = 0, leafangle < 2 * Pi(), leafangle += Pi() / 4,
xleaf = xcleaf + radleaf * Cos( leafangle );
yleaf = ycleaf + radleaf * Sin( leafangle );
// move to the new leaf ball, then draw the ball
Insert Into( global:pathLeaves, Eval List( {Eval List( {xleaf, yleaf, If( leafangle == 0, 1/*move*/, 2/*draw*/ )} )} ) );
);
);
// ditto, x0R,y0R to x1R,y1R is the trailing (right side) edge. But reversed.
Insert Into( global:pathTrunk, Eval List( {Eval List( {x1R, y1R, 0 /*control*/} )} ) );
Insert Into( global:pathTrunk, Eval List( {Eval List( {(x0R + x1R) / 2, (y0R + y1R) / 2, 3/*bezier*/} )} ) );
Insert Into( global:pathTrunk, Eval List( {Eval List( {x0R, y0R, 0 /*control*/} )} ) );
);
// these two globals are filled in by the recursive routine
global:pathTrunk = {};
global:pathLeaves = {};
size = 11; // of the trunk, radius really
treepath( 0, 0, size, Pi() / 2 ); // do the recursion
// leading move, control...this adds the left-side ground
Insert Into( global:pathTrunk, {{-size, 0, 0}}, 1 );//push control
Insert Into( global:pathTrunk, {{-size - 5, 0, 1}}, 1 );//push move
// trailing control, draw...this adds the right-side ground
Insert Into( global:pathTrunk, {{size, 0, 0}} );//push control
Insert Into( global:pathTrunk, {{size + 5, 0, 3}} );//push move
// convert the lists into matrices. It was easier to add to the lists during recursion
// but path() needs the matrix
matTrunk = Matrix( global:pathTrunk );
matLeaves = Matrix( global:pathLeaves );
New Window( "Example",
Graph Box(
X Scale( -600, 600 ),
Y Scale( -100, 1100 ),
framesize( 950, 950 ),
<<backgroundcolor( HLS Color( .66, .2, 1 ) ), // dark blue
Fill Color( HLS Color( .16, .3, .5 ) ); // brown
Path( matTrunk, 1 );
Transparency( .75 ); // play with this...
Fill Color( HLS Color( .33, .6, .8 ) ); // green
Path( matLeaves, 1 );
)
);It is a little hard to figure out what the path() function expects for a Bezier curve, but it makes sense when it is done. The first item in the list should be a move (1), and the last item should be a Bezier point (3). Two control points (0) appear between each pair of Bezier points and between the initial move and Bezier. The drawn line goes through the move (1) and Bezier (3) points. The control points (0) determine the shape of the curve; the line does not go through them but does go toward them. The code above makes the pair of control points both the same point (blue, way above). There must still be two.
See this answer for code to experiment with behavior.
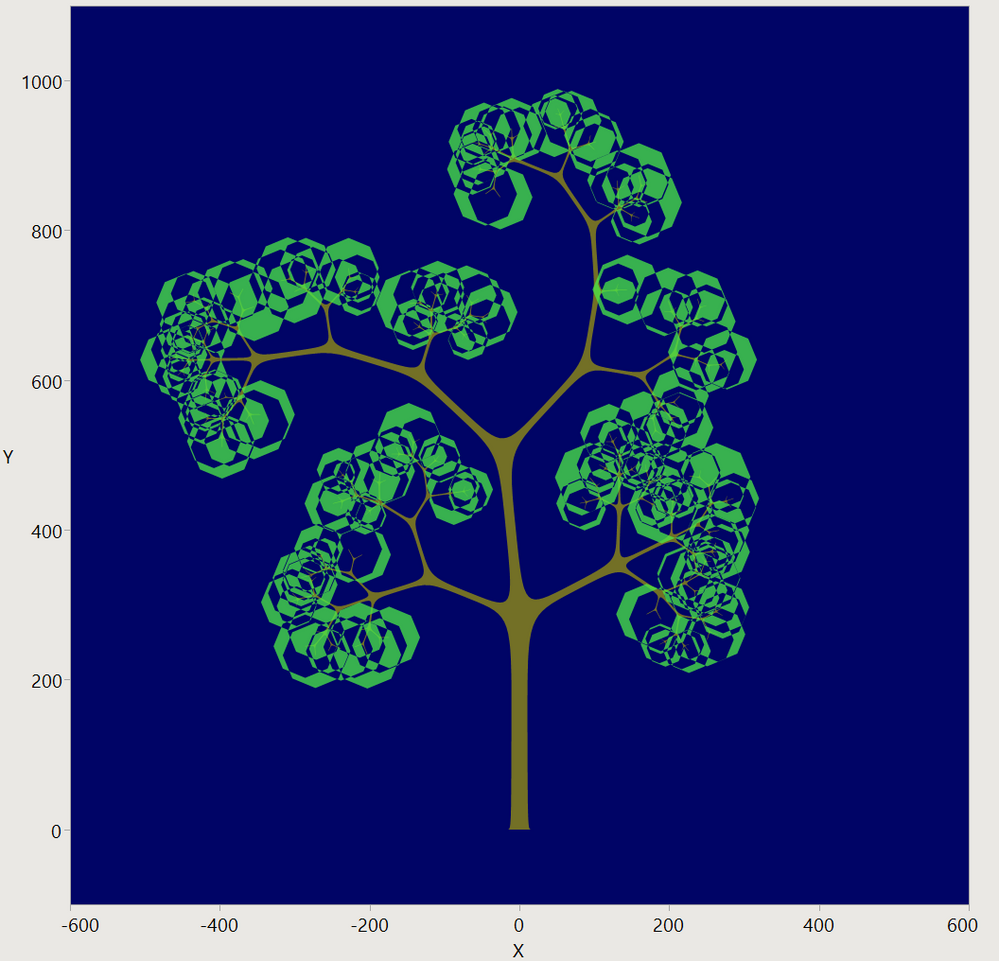
Bézier is the correct spelling. Pronunciation is harder for me. https://en.wikipedia.org/wiki/B%C3%A9zier_curve
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us
