Producing and Interpreting Basic Statistics

See how to:

• Look at box plots and statistics, as originally proposed by Mary Eleanor Spear as a way to present information about populations of people
  • Examine how box plots graphically communicate information about the central tendency and spread of data regardless of its underlying distribution
  • Deploy JMP to create box plot to understand the distribution of the data and generate some statistics for Barley Protein data

  • Interpret JMP 16 and later Notched Box Plots, where JMP uses a horizontal line for the median rather than a notch and adds a mean diamond for the mean too. 

• Use Student's t-test, as first presented by Sealy Gosset, to determine if a mean is different from a target or if two means are statistically the same, for example, if grain samples from different lots have the same (acceptable) protein content as a target value
• Perform Exploratory Data Analysis (EDA), as codified and refined by John Tukey, to look at data that have potential relationships and examine some statistics that help understand the relationships

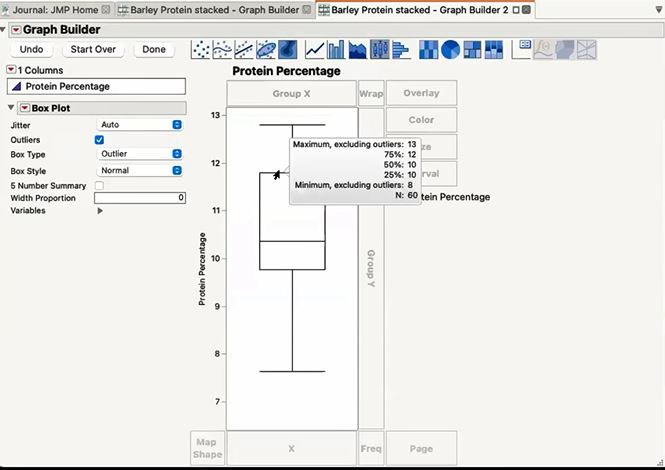Barley Box PlotBarley Box Plot

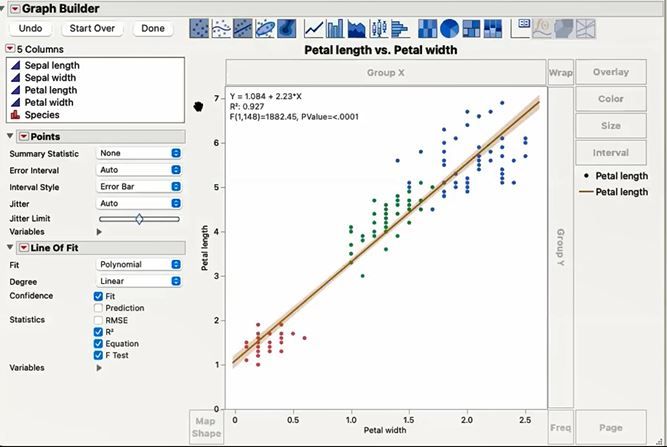Petal Length vs WidthPetal Length vs Width

Resources

• Box Plots
• JMP Statistics Knowledge Portal -  free online course in basic stats