Process analytical technology and JMP
Process analytical technology (PAT) is not new to the world, but it may be a newer concept for many, especially when it comes to using JMP to analyze and process PAT data. PAT can be part of and is o...
 Bill_Worley
Bill_Worley
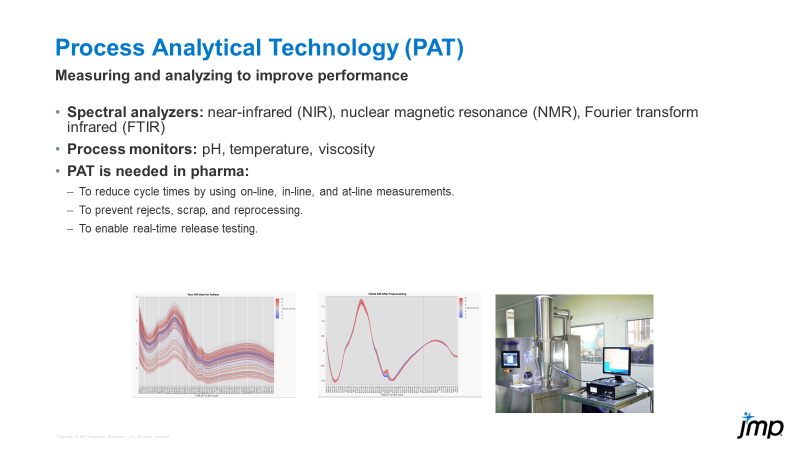
 DaeYun_Kim
DaeYun_Kim
 SamGardner
SamGardner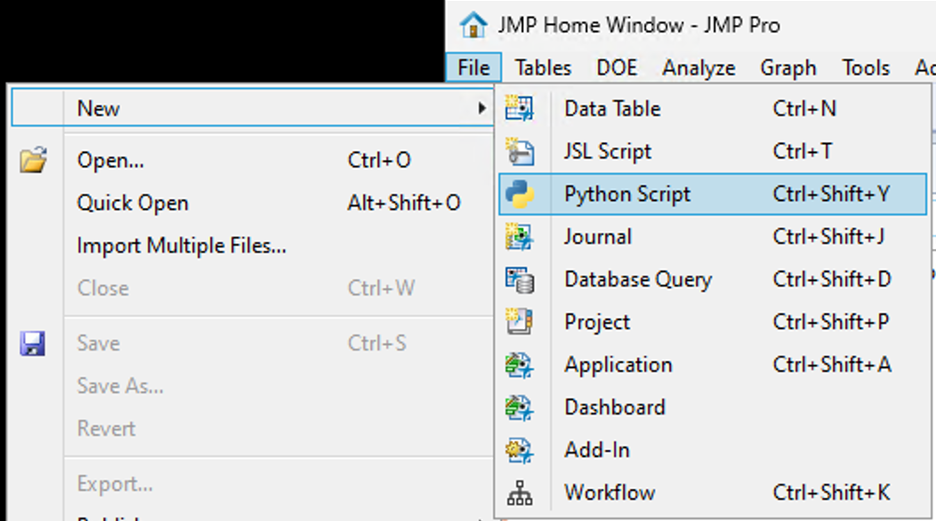
 gail_massari
gail_massari
 Valerie_Nedbal
Valerie_Nedbal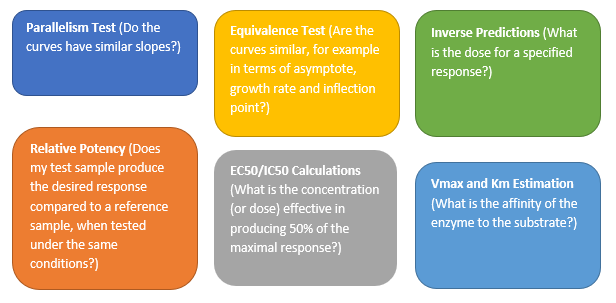
 Richard_Zink
Richard_Zink KristenBradford
KristenBradford
 Chris_Kirchberg
Chris_Kirchberg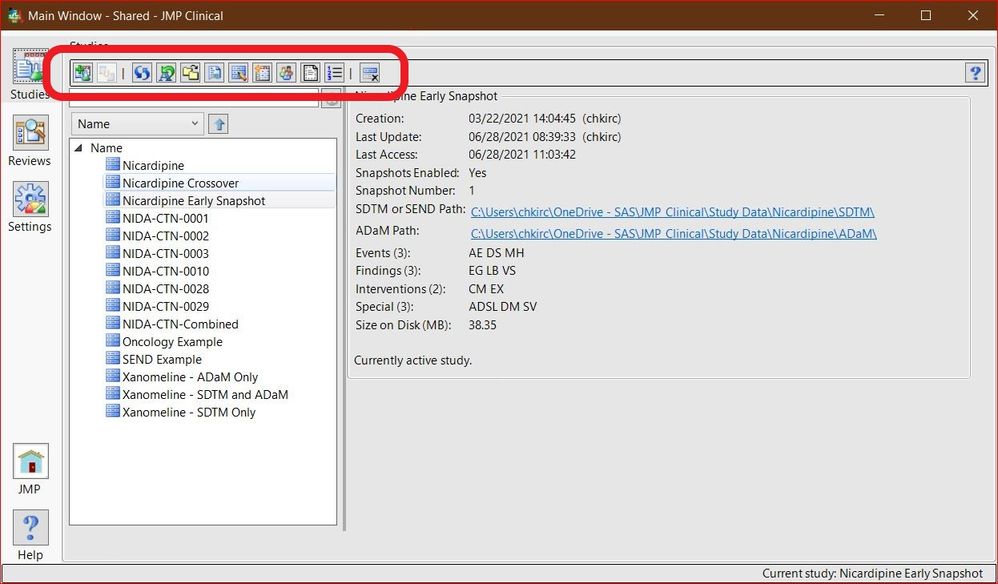
 cweisbart
cweisbart
 Paul_Nelson
Paul_Nelson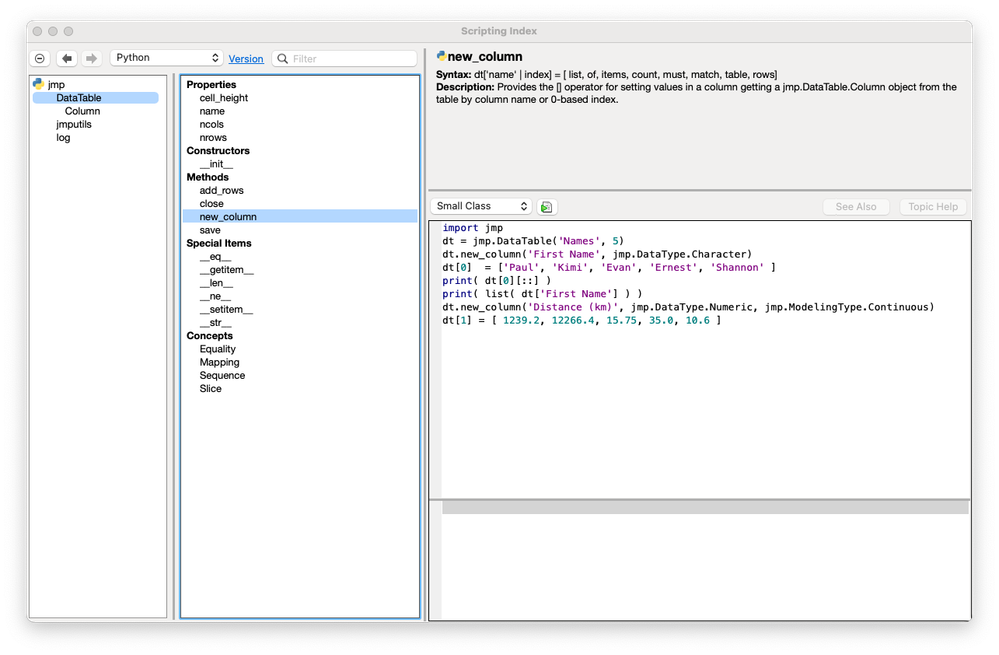
 Craige_Hales
Craige_Hales
 anne_milley
anne_milley
 Di_Michelson
Di_Michelson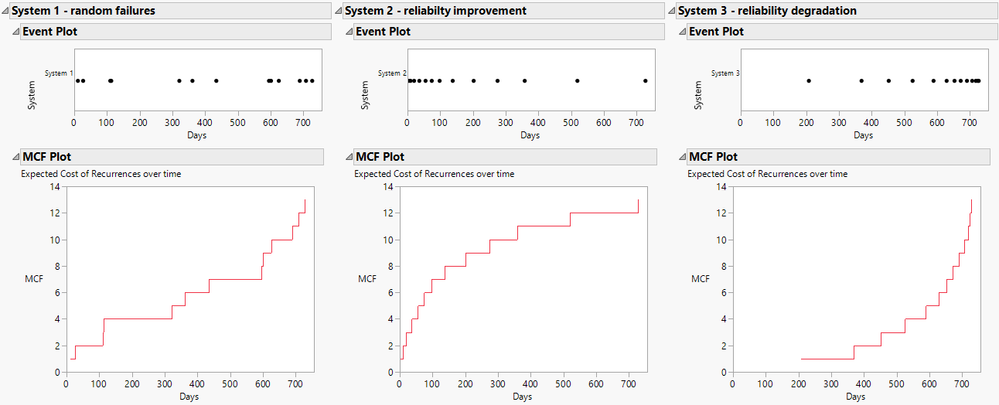
 JohnPonte
JohnPonte Masukawa_Nao
Masukawa_Nao


 Jed_Campbell
Jed_Campbell LauraCS
LauraCS MarilynWheatley
MarilynWheatley