1回30分のオムニバスセミナー「JMP 情報局」で実施したことのまとめ(第5回~第8回実施分)
JMPジャパン事業部では、今年3月から4月にかけて「JMP情報局」というセミナーを毎週火曜日、全8回で実施しました。このセミナーは、毎回30分という短時間でJMPの様々な情報をお伝えすることを目的としており、想定を上回る多くの方々にご参加いただきました。 エンディングで頂いた多くのリアクション 本ブログでは、4月に実施した第5回~第8回で実施...
 Masukawa_Nao
Masukawa_Nao

 Jed_Campbell
Jed_Campbell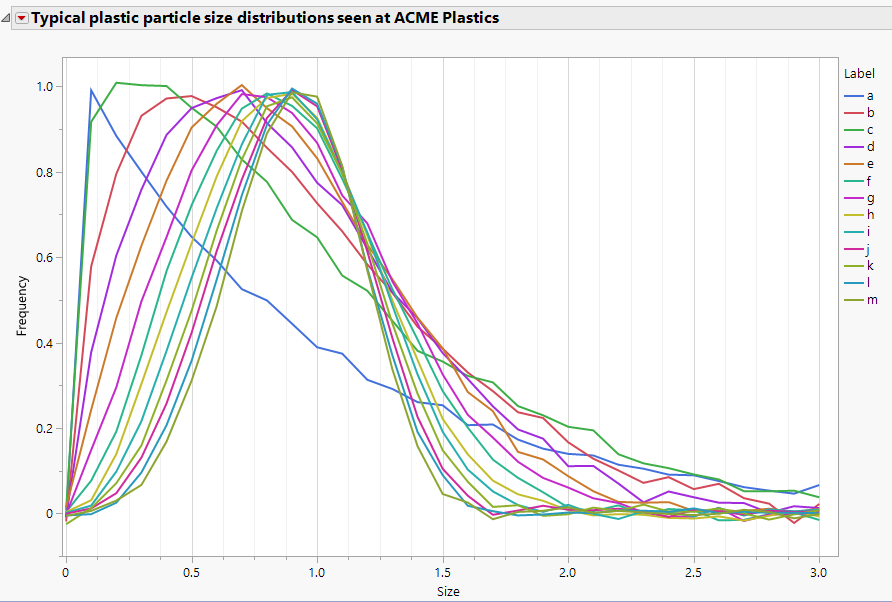
 Phil_Kay
Phil_Kay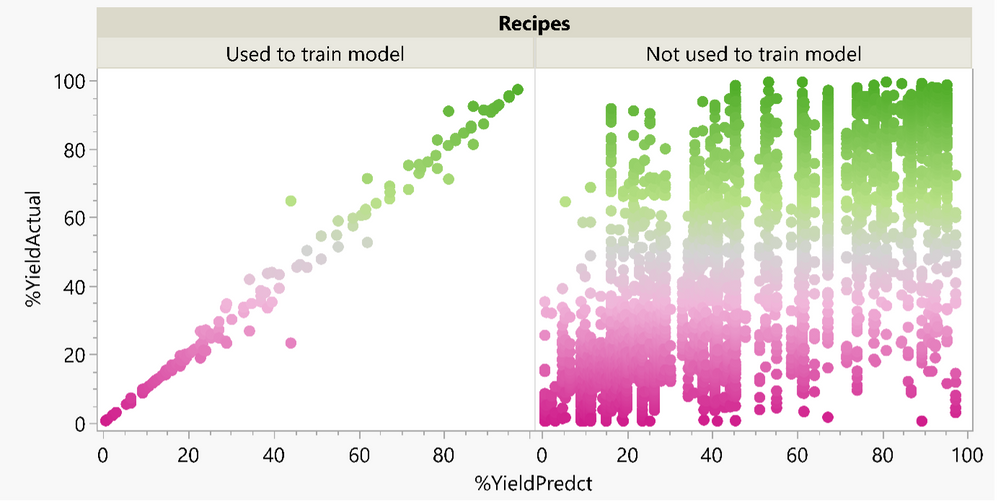
 Bill_Worley
Bill_Worley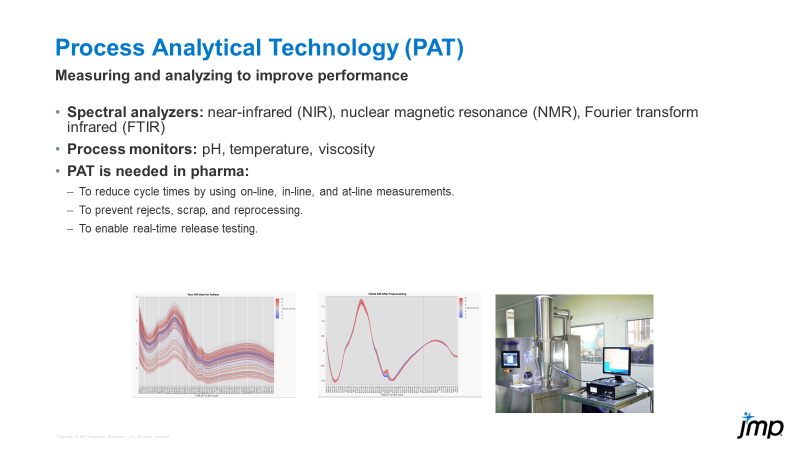
 DaeYun_Kim
DaeYun_Kim
 SamGardner
SamGardner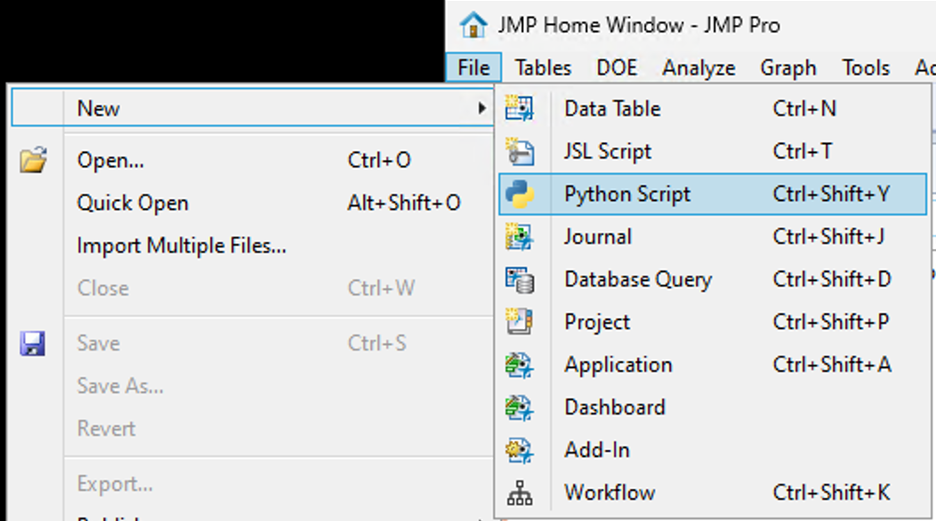
 gail_massari
gail_massari
 Valerie_Nedbal
Valerie_Nedbal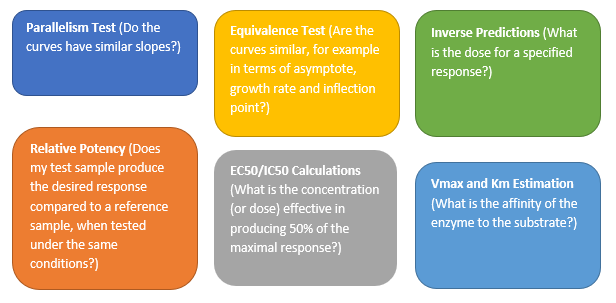
 Richard_Zink
Richard_Zink
 KristenBradford
KristenBradford
 Chris_Kirchberg
Chris_Kirchberg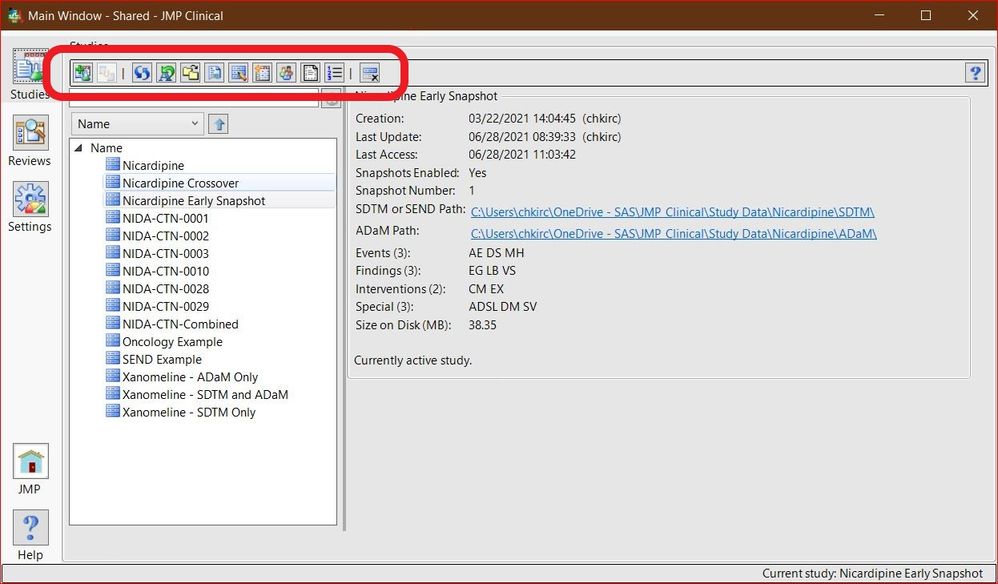
 cweisbart
cweisbart
 Paul_Nelson
Paul_Nelson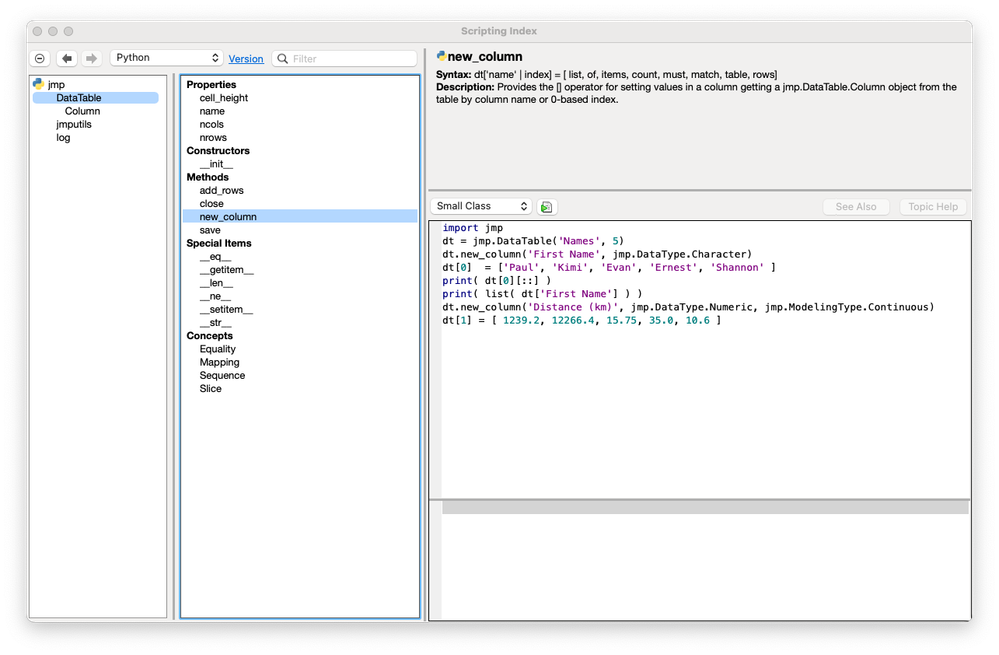
 Craige_Hales
Craige_Hales
 anne_milley
anne_milley
 Di_Michelson
Di_Michelson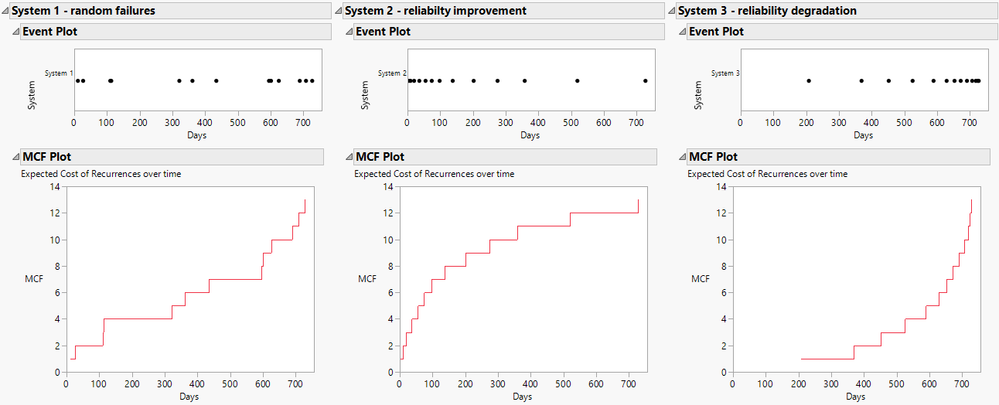
 JohnPonte
JohnPonte

