Robust Regression Using Regular JMP 18 version powered by Python Integration
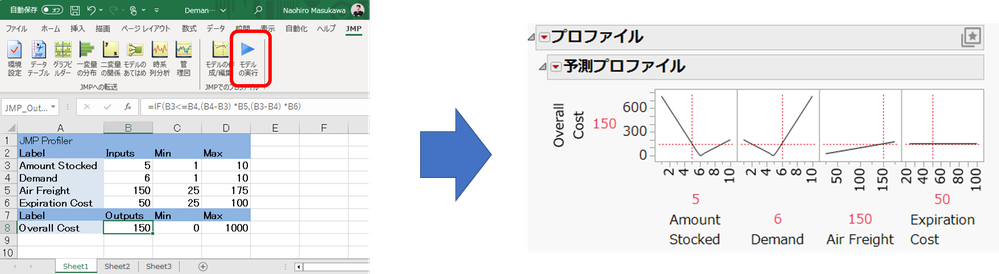
Enhance your regression analysis with the powerful combination of robust techniques and JMP 18, now featuring seamless integration with Python. Simple Case Study Here's a sample...
 DaeYun_Kim
DaeYun_Kim

 Richard_Zink
Richard_Zink
 SamGardner
SamGardner
 KristenBradford
KristenBradford
 Chris_Kirchberg
Chris_Kirchberg
 cweisbart
cweisbart
 Paul_Nelson
Paul_Nelson
 Craige_Hales
Craige_Hales
 anne_milley
anne_milley
 Di_Michelson
Di_Michelson
 JohnPonte
JohnPonte Masukawa_Nao
Masukawa_Nao


 Jed_Campbell
Jed_Campbell LauraCS
LauraCS MarilynWheatley
MarilynWheatley
 gail_massari
gail_massari