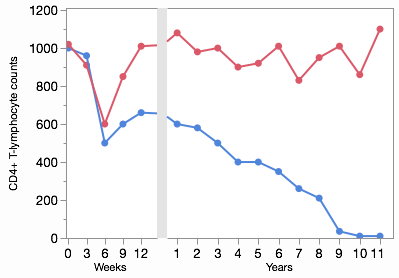
JMP is Pythonic! Enhanced Python Integration in JMP 18
JMP 18 has a new way to integrate with Python. The JMP 18 installation comes with an independent Python environment designed to be used with JMP. In addition, JMP now has a native Python editor and P...
 SamGardner
SamGardner
 KristenBradford
KristenBradford
 Chris_Kirchberg
Chris_Kirchberg
 cweisbart
cweisbart
 Paul_Nelson
Paul_Nelson
 Craige_Hales
Craige_Hales
 anne_milley
anne_milley
 Di_Michelson
Di_Michelson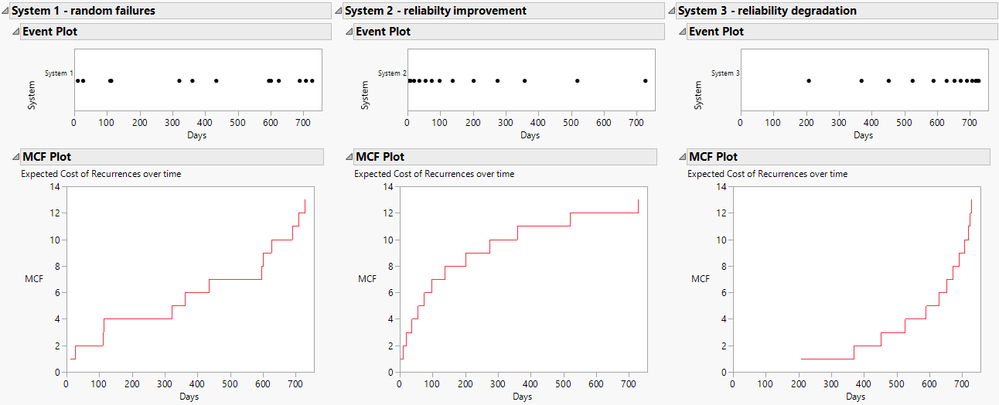
 JohnPonte
JohnPonte
 Masukawa_Nao
Masukawa_Nao


 Jed_Campbell
Jed_Campbell LauraCS
LauraCS MarilynWheatley
MarilynWheatley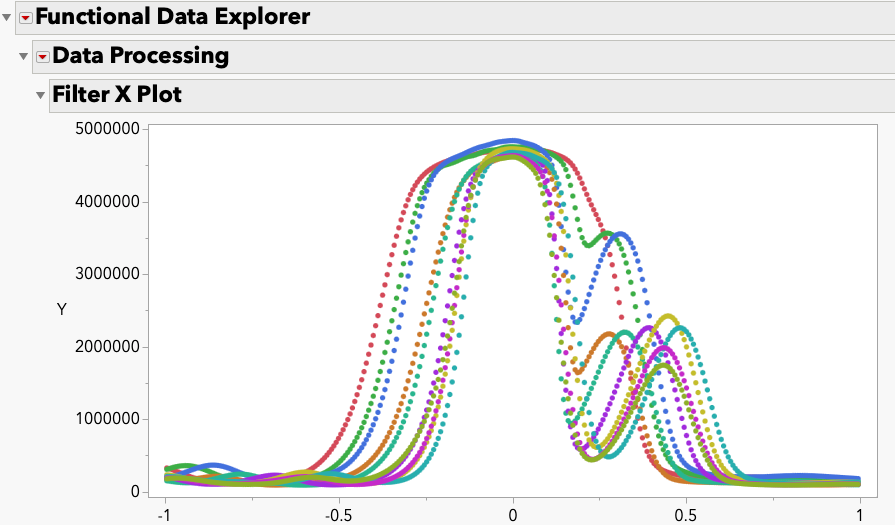
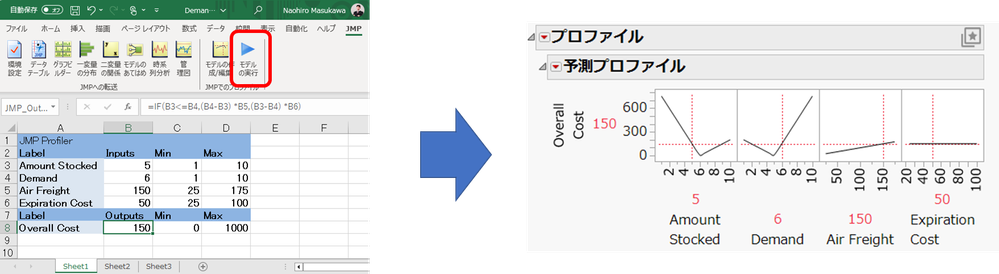
 gail_massari
gail_massari carla_paquet1
carla_paquet1
 XanGregg
XanGregg