Analytics with Confidence 3: Introducing Validation
Welcome back to Analytics with Confidence. In this series, I am exploring the key to success with modern data analytics: validation. In the first and second posts we discussed general...
 Phil_Kay
Phil_Kay
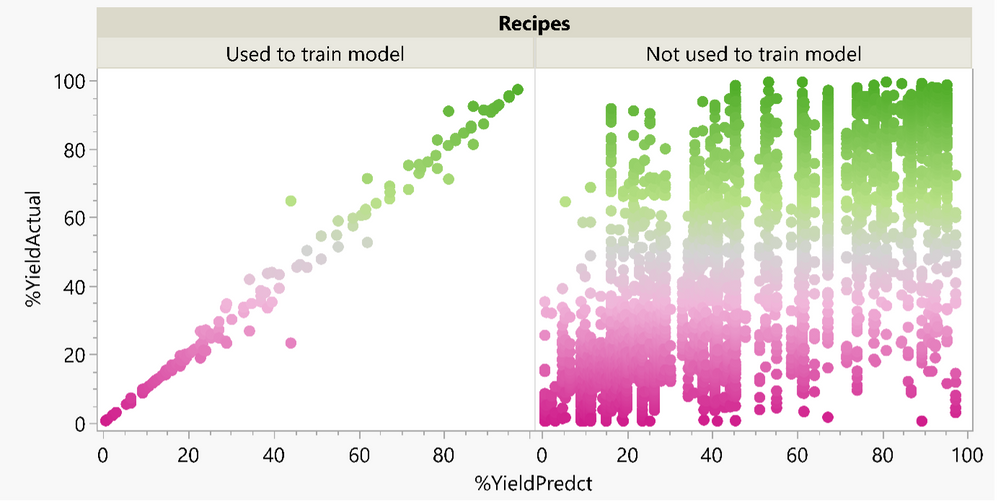
 Bill_Worley
Bill_Worley
 DaeYun_Kim
DaeYun_Kim
 SamGardner
SamGardner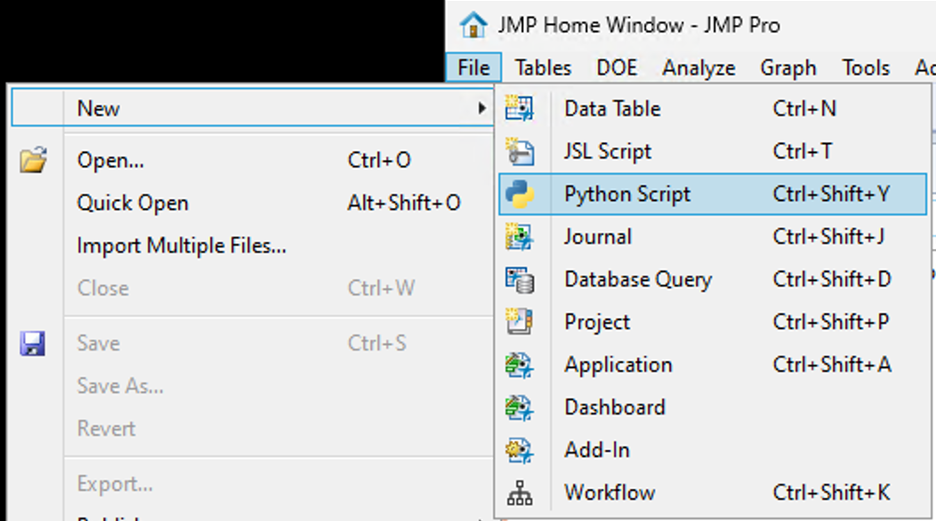
 gail_massari
gail_massari
 Valerie_Nedbal
Valerie_Nedbal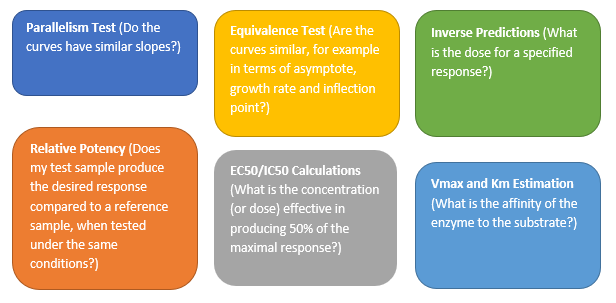
 Richard_Zink
Richard_Zink
 KristenBradford
KristenBradford
 Chris_Kirchberg
Chris_Kirchberg
 cweisbart
cweisbart
 Paul_Nelson
Paul_Nelson
 Craige_Hales
Craige_Hales
 anne_milley
anne_milley
 Di_Michelson
Di_Michelson
 JohnPonte
JohnPonte Masukawa_Nao
Masukawa_Nao


 Jed_Campbell
Jed_Campbell LauraCS
LauraCS